

Cell Morphodynamics via Phase Field Dynamics Model
Received date: 2013-03-11
Online published: 2013-05-06
Supported by
Project supported by the National Natural Science Foundation of China (Nos. 21004018, 21274038) and the Fundamental Research Funds for the Central Universities.
Cell motion is a complex biological process that involves the cooperative interactions between the cytoskeleton and cell membrane, and these interactions generally include these interactive energies generated from the surface tension and the bending elastic energy of the cell membrane, the “protrusive” and “contractile” forces separately driven by actin polymerization into cytoskeletons and myosin contraction, and the adhesion between the cell and the substrate. Herein, one computational model based on the phase field method and the reaction-diffusion model is subsequently developed to describe this complicated biological process, coupling the cell movement and cell morphologenis with the dynamic behaviors of actin assemble into actin filaments, the physiological functions of myosin, and the interaction between the cell and the substrate. In the computational model for cell motion, the moving boundary with physical membrane properties is proposed to numerically solve the problem involved in the computational efficiency. The fish keratocytes, fast moving cells that maintain their morphology, are applied in the present study, and the related system parameters are chosen. The steady state and movement velocity of cells are obtained with a wide range of aspect ratios and movement velocities in the computational model, which are found to be well in agreement with the associated experimental results in vitro. In addition, the dependences of the movement velocity and the steady state of the cells are in detail studied on system parameters that are the concentrations of the actin and myosin, as well as the actin rate constants. It will be straightforward to extend this method to more complicated systems, such as cell contraction, cell division, and cell movement in actin flow and shear flow.
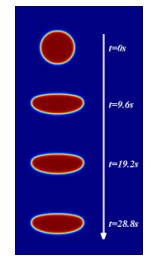
Key words: cell motion; cell morphology; actin; myosin; phase field method
Liu Zhuan , Guo Kunkun . Cell Morphodynamics via Phase Field Dynamics Model[J]. Acta Chimica Sinica, 2013 , 71(08) : 1183 -1188 . DOI: 10.6023/A13030266
[1] Mogilner, A. J. Math. Biol. 2009, 58, 105.
[2] Phillips, R.; Kondev, J.; Theriot, J. Physical Biology of The Cell. Garland Science Publishing, New Haven, 2008, pp. 569~586.
[3] Fournier, M. F.; Sauser, R.; Ambrosi, D.; Meister, J. J.; Verkhovsky, A. B. J. Cell Biol. 2010, 188, 287.
[4] Pollard, T. D. J. Cell Biol. 1986, 103, 2747.
[5] Alamo, J. C.; Meili, R.; Alonso-Latorre, B.; Rodríguez-Rodríguez, J.; Aliseda, A.; Firtel, R. A.; Lasheras, J. C. PNAS. 2007, 104, 13343.
[6] Verkhovsky, A. B.; Svitkina, T. M.; Borisy, G. G. Curr. Biol. 1999, 9, 11.
[7] Guo, K. K.; Han, W. C. Acta Chim. Sinica. 2011, 69, 145 (in Chinese).
(郭坤琨, 韩文驰, 化学学报, 2011, 69, 145.)
[8] Gracheva, M. E.; Othmer, H. G. Bull. Math. Biol. 2004, 66, 167.
[9] Larripa, K.; Mogilner, A. Phys. A. 2006, 372, 113.
[10] Carlsson, A. E. New J. Phys. 2011, 13, 073009.
[11] Rubinstein, B.; Fournier, M. F.; Jacobson, K.; Verkhovsky, A. B.; Mogilner, A. Biophys. J. 2009, 97, 1853.
[12] Barnhart, E. L.; Lee, K. C.; Keren, K.; Mogilner, A.; Theriot, J.A. PLOS. Biol. 2011, 9, e1001059.
[13] Wolgemuth, C. W.; Stajic, J.; Mogilner, A. Biophys. J. 2011, 101, 545.
[14] Yang, L.; Effler, J. C.; Kutscher, B. L.; Sullivan, S. E.; Robinson, D. N.; Iglesias, P. A. BMC. Syst. Biol. 2008, 2, 68.
[15] Shao, D. Y.; Rappel, W. J.; Levine, H. Phys. Rev. Lett. 2010, 105, 108104.
[16] Chan, C. E.; Odde, D. J. Science 2008, 322, 1687.
[17] Buenemann, M.; Levine, H.; Rappel, W. J.; Sander, L.M. Biophys. J. 2010, 99, 50.
[18] Long, W. Y.; Lv, D. L.; Xia, C.; Pan, M. M.; Cai, Q. Z.; Chen, L. L. Acta Physica. Sinica. 2009, 58, 7802 (in Chinese).
(龙文元, 吕冬兰, 夏春, 潘美满, 蔡启舟, 陈立亮, 物理学报, 2009, 58, 7802.)
[19] Du, Q.; Liu, C.; Wang, X. J. Comput. Phys. 2006, 212, 757.
[20] Lowengrub, J. S.; Ratz, A.; Voigt, A. Phys. Rev. E. 2009, 79, 031926.
[21] Helfrich, W. Z. Naturforsch 1973, 28, 693.
[22] Shao, D. Y.; Rappel, W. J.; Levine, H. PNAS. 2012, 109, 6851.
[23] Theriot, J. A.; Mitchison, T. J. Nature 1991, 352, 126.
[24] Kerenet, K.; Pincus, Z.; Allen, G. M,; Barnhart, E. L.; Marriott, Gerard.; Mogilner, Alex.; Theriot, J. A. Nature 2008, 453, 475.
[25] Mogilner, A.; Oster, G. Curr. Biol. 2003, 13, R721.
[26] Koenderink, G. H.; Dogic, Z.; Nakamura, F.; Bendix, P. M.; Mackintosh, F. C.; Hartwing, J. H.; Stossel, T. P.; Weitz, D. A. PNAS. 2009, 106, 15192.
[27] Didry, D.; Carlier, M. F.; Pantaloni, D. J. Biol. Chem. 1998, 273, 25602.
[28] Wakatsuki, T.; Wysolmerski, R. B.; Elson, E. L. J. Cell Sci. 2003, 116, 1617.
[29] Biben, T.; Kassner, K.; Misbah, C. Phys. Rev. E. 2005, 72, 041921.
[30] Ramamurthy, B.; Yengo, C. M.; Straight, A. F.; Mitchison, T. J.; Sweeney, H. L. Biochemistry 2004, 43, 14832.
[31] Simson, R.; Wallraff, E.; Faix, J.; Niewohner, J.; Gerisch, G.; Sackmann, E. Biophys. J. 1998, 74, 514.
/
| 〈 |
|
〉 |