SIOC 中文
ACS
Adv search

Acta Chimica Sinica >

2025 , Vol. 83 >Issue 9: 1006 - 1012

DOI: https://doi.org/10.6023/A25050197

Article

Relaxation and Thermal Transition of Nanoscale Polyimide Ultrathin Films★

  • Quanyin Xu ,
  • Xinyang Shi ,
  • Jintian Luo ,
  • Biao Zuo , *
Expand
  • School of Chemistry and Chemical Engineering, Zhejiang Sci-Tech University, Hangzhou 310018, China
* E-mail:

★ For the VSI “Rising Stars in Chemistry”.

Received date: 2025-05-29

  Online published: 2025-07-03

Supported by

National Natural Science Foundation of China(22303084)

National Natural Science Foundation of China(52373025)

Fold

Abstract

Polyimide (PI) films are widely used in semiconductor packaging due to their excellent properties, including low dielectric constant, high temperature resistance, and enhanced thermal and chemical stability. In recent decades, the development of modern nanotechnology has led to devices being downsized to the nanoscale, and packaging these nanodevices would require ultrathin films of PI. Understanding the thermal transition and molecular relaxation of the PI ultrathin films is essential for high-quality microelectronic packaging. Although the dynamics of bulk PI have been extensively studied using techniques such as broadband dielectric spectroscopy (BDS) and dynamic mechanical analysis (DMA), the impact of reduced film thickness on these dynamics remains unclear. In this study, we used temperature-variable spectroscopic ellipsometry to examine the thermal expansion and molecular relaxation of PI films as thin as 6 nm, and concurrently, the bulk dynamics of PI were investigated using BDS and DMA for comparison purposes. The PI films were prepared by the heat imidization of poly(amide acid) films, which were polymerized using biphenyltetracarboxylic diandhydride (BPDA) and 4,4'-oxydianiline (ODA). In 300-nm-thick films, we observed the α-relaxation arising from the segmental cooperative rearrangement, and the β-relaxation originating from phenyl ring motion at approximately 260 ℃ (Tα) and 99 ℃ (Tβ), respectively. As the film thickness decreased below 100 nm, Tα decreased. Specifically, Tα decreased by 30 ℃ for 6-nm PI films. In contrast, Tβ remains unchanged in the ultrathin films, indicating a thickness-independent β-relaxation. Furthermore, the coefficients of thermal expansion increased remarkably with a reduction in film thickness across various temperature ranges (i.e., T<Tβ, Tβ<T<Tα, and T>Tα), indicating that ultrathin PI films are more sensitive to temperature variations than bulk samples. Such observation of the thickness-dependent thermal expansivity and Tα of ultrathin PI films provide a deep understanding of the effects of nanoconfinement on the dynamics of polymers with rigid chain backbones, which is also meaningful for designing and fabricating stable nano-devices based on ultrathin PI films.

Key words： polyimide; relaxation; ellipsometry; thermal expansion; nanoconfinement

Cite this article

Quanyin Xu , Xinyang Shi , Jintian Luo , Biao Zuo . Relaxation and Thermal Transition of Nanoscale Polyimide Ultrathin Films★[J]. Acta Chimica Sinica, 2025 , 83(9) : 1006 -1012 . DOI: 10.6023/A25050197

1 引言

聚酰亚胺(Polyimide, PI)薄膜因其优异的耐高温、高绝缘及化学稳定性等性能被广泛应用于光电器件、生物传感、半导体芯片封装等战略新兴领域, 素有“黄金薄膜”之称[1-9]. 随着纳米技术的迅猛发展, 光电设备向轻薄化、小型化及高集成化方向演化; 借助光刻技术, 人们已成功将纳米级厚度的PI超薄膜用于电子封装中的介电材料[10]. 然而, 当高分子薄膜厚度降低至纳米尺度, 尤其是接近高分子链尺寸时, 其性能会偏离本体性质[11-15], 表现出纳米受限效应. 例如, 厚度在100 nm以下的聚苯乙烯薄膜具有比本体更低的玻璃化转变温度(Tg)[16-17]、更快松弛速率[18-19]和更低黏度[20-21], 致使材料易于发生去润湿等界面失稳现象[22-24]; 此外, 纳米级的聚甲基丙烯酸薄膜的热膨胀系数随着膜厚的降低而增大[25-26], 使薄膜的尺寸稳定性降低而造成材料失效. 这些都严重地限制了材料的实际应用. 因此, 研究和阐明受限状态下PI超薄膜的分子松弛行为, 对优化微纳精密器件的结构设计和性能调控具有重要意义.
过去三十年间, 纳米聚合物薄膜松弛动力学受到广泛关注; 然其研究主要集中于聚苯乙烯[16-18]、聚甲基丙烯酸甲酯[25-27]、聚醋酸乙烯酯[28]等为代表的柔性高分子; 而对PI等刚性高分子体系的研究甚少. 另一方面, Wang等[29-30]发现聚咔唑类(如PCDTBT)等刚性共轭高分子的Tg随膜厚的降低而减小; Bradley等[31]却发现聚9,9-二辛基芴的Tg随膜厚降低出现先升高后降低的非单调趋势; 而Fytas等[32]发现了纳米级聚酰亚胺薄膜的弹性模量不依赖于厚度, 这说明刚性高分子具有丰富且复杂的纳米受限行为. 芳香型聚酰亚胺作为刚性聚合物的典型代表, 在电子封装领域的应用占据主导地位[33]. 借助于宽频介电谱(BDS)与动态力学分析(DMA)等常规动力学表征技术, 其本体多尺度松弛动力学行为已基本明确, 包括: 链段协同运动相关的α松弛[34-35]、苯环的振动或旋转相关的β松弛[34-36]、涉及极性基团(如C=O)局部振动的γ松弛[35-36]. 但受制于超薄膜纳克级的样品量带来的反馈信号弱、测量难等问题, 上述方法难以应用于PI纳米超薄膜的测量.
薄膜受热发生的体积膨胀是分子运动的宏观表现; 故而可以通过研究热膨胀变化分析材料松弛和热转变[37-38]. 椭圆偏振光谱(Ellipsometry)可以精准测量纳米薄膜的厚度, 其分辨率达到亚纳米级; 结合控温热台, 可以实现薄膜热膨胀行为并测量, 是研究纳米超薄膜松弛的有效手段[39]. 基于此, 本文制备了联苯四甲酸二酐-二氨基二苯醚聚酰亚胺薄膜, 通过研究PI纳米超薄膜的热膨胀来研究它的松弛行为, 并讨论其随厚度的变化. 结果发现, 随着薄膜厚度降低, PI纳米薄膜的α松弛转变温度(Tα)减小, 而β松弛转变温度(Tβ)几乎不变; 并伴随着薄膜的膨胀系数增大.

2 结果与讨论

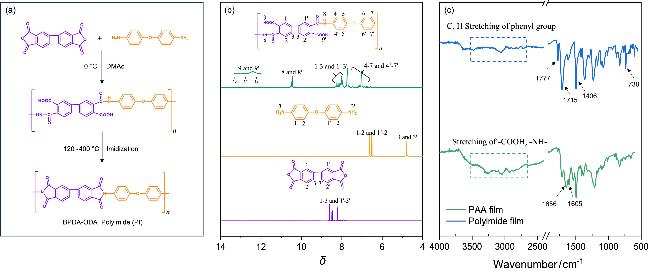
2.1 聚酰亚胺膜的合成与结构表征

如图1a所示, 采用两步法制备聚酰亚胺薄膜[40-42]. 首先利用联苯四甲酸二酐(BPDA)与二氨基二苯醚(ODA)的缩聚反应制备聚酰胺酸(PAA)溶液, 利用浇铸及旋涂法制备不同厚度(6 nm~80 μm)的PAA薄膜, 然后利用高温亚胺化反应将PAA薄膜转变聚酰亚胺(PI)薄膜.
图1 (a)制备BPDA-ODA型聚酰亚胺(PI)薄膜的路径图, (b)聚酰胺酸(PAA)的1H NMR谱图和(c) PAA与PI薄膜的FT-IR谱图

Figure 1 (a) Synthesis route for the BPDA-ODA polyimide (PI) films, (b) 1H NMR spectrum of poly(amido acid) (PAA) and (c) FT-IR spectra of PAA and PI films

通过核磁共振氢谱(1H NMR)可以确认聚酰胺酸(PAA)的成功合成[43-44]. 如图1b所示, 谱图中δ 12~14处的宽峰归属于羧酸基团(-COOH)的质子信号, δ 10.5附近的特征峰来自于酰胺键(-C(O)NH)中的质子共振. 此外, δ 7.8~8.5与6.5~7.8范围内的信号峰分别来源于BPDA和ODA的芳香环氢原子. 通过对热处理前后PAA薄膜的红外光谱进行对比, 可以确认PAA薄膜经过高温亚胺化已充分转变为PI. 如图1c所示, 未亚胺化的PAA薄膜在1656和1605 cm−1处显示出酰胺基团的典型吸收峰, 经高温亚胺化后, 上述位置的峰消失, 取而代之的是1777 cm−1(不对称C=O伸缩振动)和1715 cm−1(对称C=O伸缩振动)处的酰亚胺环羰基吸收峰. 同时, 730 cm−1(酰亚胺C—N的弯曲振动)及1406 cm−1(酰亚胺环中C—N伸缩振动)处吸收峰的出现, 以及2500~3500 cm−1处羧基和亚氨基吸收峰的完全消失[45], 表明PAA已完全转化为聚酰亚胺. 上述结果表明我们成功制备了不同厚度的平整的PI薄膜样品.

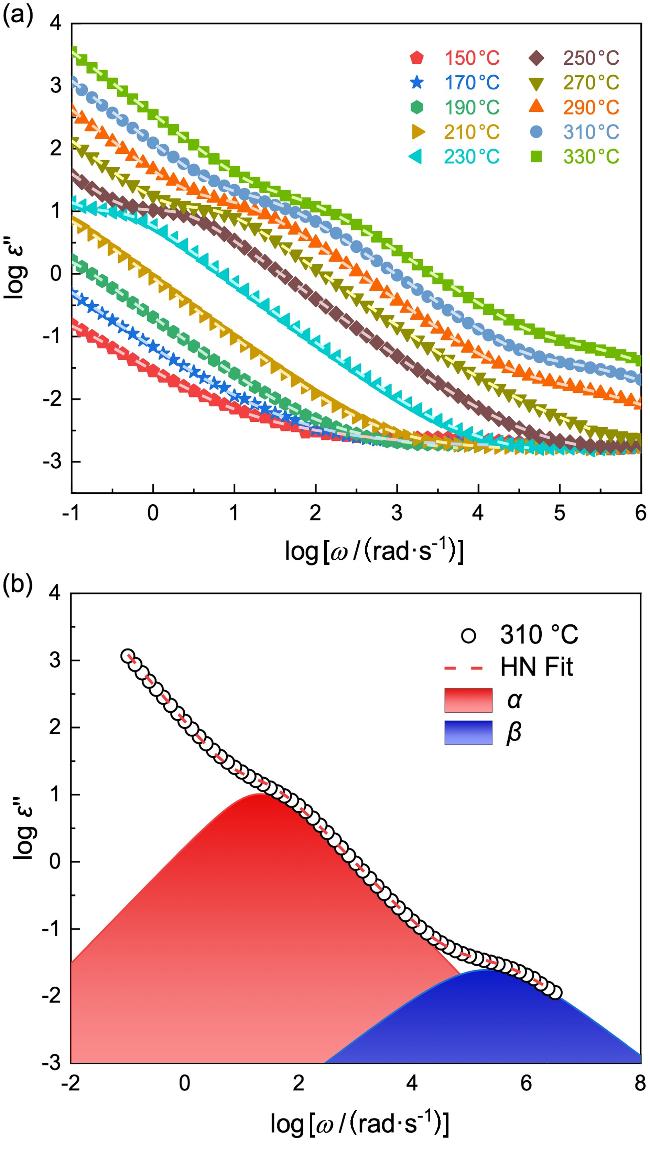
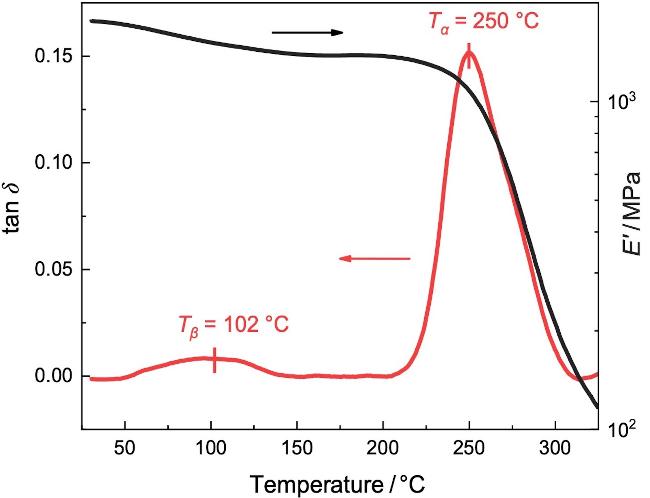
2.2 聚酰亚胺的本体松弛

对微米级厚度PI薄膜进行介电松弛和动态热机械表征, 进而研究本体PI的松弛行为. 图2a展示的是80 μm PI膜在不同温度下(150~330 ℃)的宽频介电谱(Broadband dielectric spectroscopy, BDS). ε"代表介电损耗、ω为角频率. 可以看到, 在相同温度下, ε"随ω的减小而增大. ε"(ω)包含了PI分子多级松弛的贡献, 包括链段运动主导的α松弛和局部基团运动的次级松弛等. 此外, 随着温度的升高, ε"(ω)向高频移动, 说明PI膜的松弛速率随温度升高而加快.
图2 (a) 不同温度下PI膜的介电损耗谱, (b) T=310 ℃时的介电损耗谱及其HN函数拟合结果(虚线). 膜厚为80 μm

Figure 2 (a) Dielectric loss of polyimide film at different temperatures, (b) Dielectric loss at T=310 ℃ and the dashed line shows the HN function fitting. Thickness of the film is 80 μm

为了定量研究不同松弛模式的贡献, 利用Havriliak- Negami (HN)模型(公式1)[46]对图2中的介电损耗谱进行拟合, 如
$\varepsilon _{\text{NH}}^{*}(\omega ){{\varepsilon }_{\infty }}\sum\limits_{j=\alpha,\beta,\cdots }{\frac{\Delta {{\varepsilon }_{j}}}{{{[1{{(i\omega {{\tau }_{j}})}^{{{m}_{j}}}}]}^{{{n}_{j}}}}}}\frac{{{\sigma }_{ac}}}{i{{\varepsilon }_{0}}\omega }$
其中ε0=8.85×10−12 F/m为真空介电常数; ε∞和σac分别是高频介电常数和低频下的交流电导; 中间各项分别对应各松弛模式(标记为j, 对应着α和β等松弛模式)的介电强度(Δεj)和特征松弛时间(τj), 及其它们各自的对称(mj)和不对称增宽参数(nj). εHN"(ω)为εHN*(ω)的虚部. 图2为利用公式1对310 ℃下ε"(ω)的拟合结果. 拟合结果分离出了α和β松弛两种模式, 它们的特征松弛时间分别为τα=0.047 s和τβ=4.8×10−6 s; 同时, 两个松弛峰都仅表现出对称增宽, mα=0.87, mβ=0.65, nα=nβ=1.
利用公式1对不同温度下的ε"(ω)进行拟合结果(见图2a中的虚线), 从而得到不同温度下τα和τβ, 见图3. 可见, PI膜的τα具有更强的温度依赖性, 符合Vogel- Fulcher-Tammann (VFT)关系[47-49]的描述, 即
${{\tau }_{\alpha }}{{\tau }_{\alpha 0}}\exp \frac{D{{T}_{V}}}{T{{T}_{V}}}$
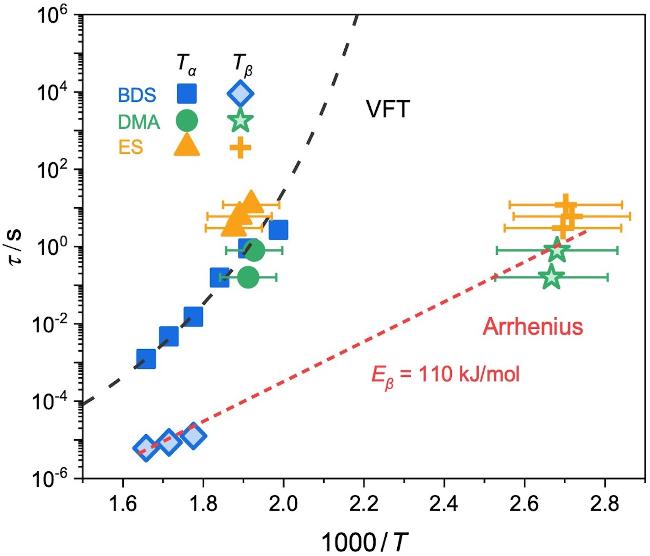
图3 PI膜的α和β松弛时间与1000/T的关系图. 黑色虚线为VFT方程拟合的结果(公式2), 红色虚线为Arrhenius方程拟合的结果(公式3)

Figure 3 α and β relaxation time plotted as a function of the inverse temperature for polyimide film. The dotted lines (red and black) are the fitting of the data to the VFT and Arrhenius equation, respectively

其中τα,0、D和TV (Vogel温度)是拟合参数. 这表明α松弛模式确实由链段运动所主导, 具有协同运动的特性[50-51]; 松弛激活能随温度降低而增加. 然而, τβ的温度依赖性则符合Arrhenius关系[35], 即
${{\tau }_{\beta }}{{\tau }_{\beta 0}}\exp \frac{{{E}_{\beta }}}{RT}$
其中R=8.3145 J/(K•mol), Eβ为表观β松弛活化能. 拟合结果显示Eβ≈110 kJ/mol, 与文献报道的结果一致[34-36]; 这反映了β松弛来源于芳香族聚酰亚胺中芳环的局部振动.
动态力学分析(Dynamic mechanical analysis, DMA)能测定PI膜在正弦交变载荷下的力学响应和损耗, 从而表征高分子松弛行为[34,52]. 图4为通过升温过程中上述80 μm PI膜的储能模量(E')和损耗正切角(tan δ)的变化. 如图所示, PI膜的E'随温度升高出现了两次台阶式下降: 分别在50~150 ℃和250~300 ℃处; 同时, 对应着两个tan δ的损耗峰. 它们可以分别归属于升温过程中PI薄膜内的基团局部运动对应的β松弛模式和链段运动所贡献的α松弛模式. 特征松弛温度(Tα和Tβ)可由tan δ峰值温度来确定, 即Tβ=102 ℃和Tα=250 ℃. 此外, 损耗峰峰值处, 材料的松弛时间等于实验测量时间; DMA的实验时间由其频率决定, 即: τDMA=1/2πfDMA. 那么, 可以将DMA确定的α松弛(Tα,DMA, τDMA)和β松弛(Tβ,DMA, τDMA)汇总到图3中(见图中的绿色符号). 可见, DMA的结果与BDS结果很好吻合, 也验证了BDS和DMA二者测量结果的准确性.
图4 PI膜的储能模量(E')及损耗因子(tan δ)的温度依赖性. PI的膜厚为80 μm

Figure 4 Temperature dependence of storage modulus (E') and loss factor (tan δ) of polyimide film. Thickness of the film is 80 μm

另一方面, PI薄膜受热会发生膨胀, 导致膜厚随温度升高而增大. 热膨胀能力用热膨胀系数(k)表示. 温度升高将加速分子运动; 当薄膜内某一特定运动模式被激活, 材料的k也会随之增大. 利用变温椭圆偏振光谱(Ellipsometry, ES)对300 nm厚度PI膜的厚度(h)随温度的变化进行了研究, 结果见图5. PI薄膜表现出典型的线性膨胀行为; 薄膜厚度随温度升高而线性增厚. 为了定量描述PI薄膜的热转变, 对h~T曲线求导得到薄膜k, 即
$k\frac{1}{h}\centerdot \frac{dh}{dT}$
图5 (a) 300 nm PI膜的厚度与(b)膨胀系数的温度依赖性

Figure 5 (a) Temperature dependence of the thickness and (b) the thermal expansion coefficient of the 300 nm thick polyimide film

图5b显示了PI薄膜的k随温度上升的变化行为. 可以看到, 当T<70, 120<T<240和T>270 ℃范围内, k维持不变, 分别为k1≈0.00013、k2≈0.00019、k3≈0.00058 ℃−1. 而在100和260 ℃附近, k增大, 对应着两个松弛转变. 在100 ℃附近时, PI薄膜的k增幅较小, k2≈1.5k1, 说明此温度下所激活的分子运动能力较弱, 对应局域小尺度运动的β松弛, 即Tβ,ES≈99 ℃; 而在260 ℃附近时, k3≈3k2, 表明有较大尺度的运动模式被激活, 对应着链段运动的α松弛. Tβ,ES≈99 ℃和Tα,ES≈260 ℃与DMA测得α和β松弛温度一致. 同时, 变温椭圆偏振光谱的实验时间尺度由线性升温速率(q)决定, 即τES=1/q. 那么, 可将变温椭圆偏振光谱所确定的α松弛(Tα,ES, τES)和β松弛(Tβ,ES, τES)汇总到图3中(见图中的绿色符号). 由图3可见, 椭圆偏振光谱(ES)的测量结果与常规方法BDS和DMA的测量结果基本一致. 这说明变温椭圆偏振光谱能够准确测定本体PI膜的多尺度松弛动力学.

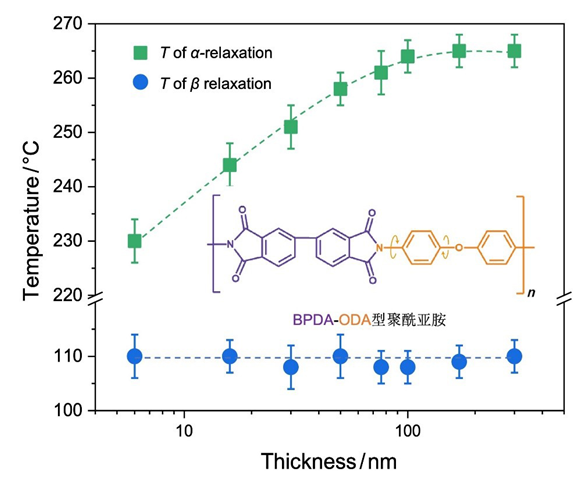
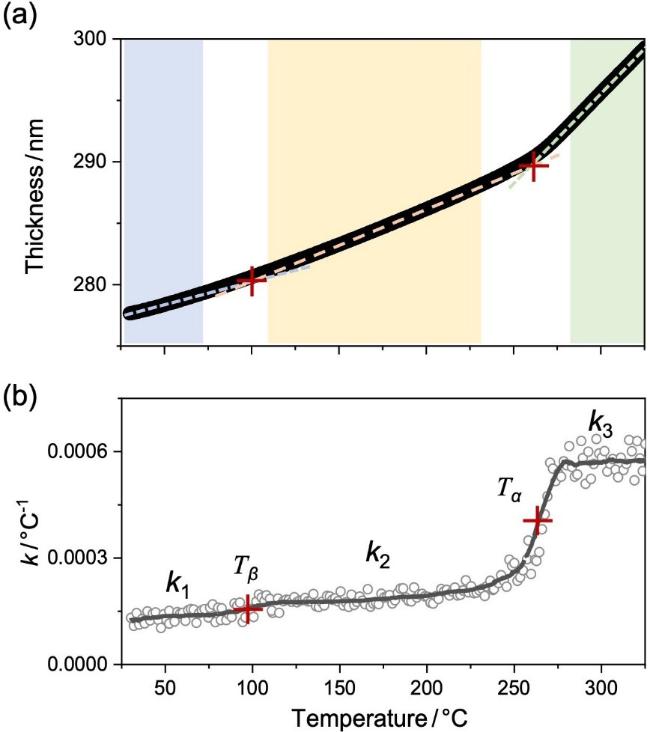
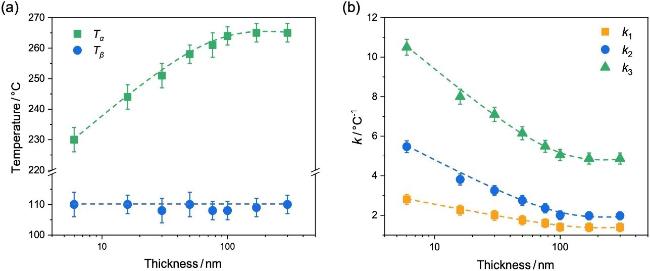
2.3 纳米聚酰亚胺超薄膜的松弛

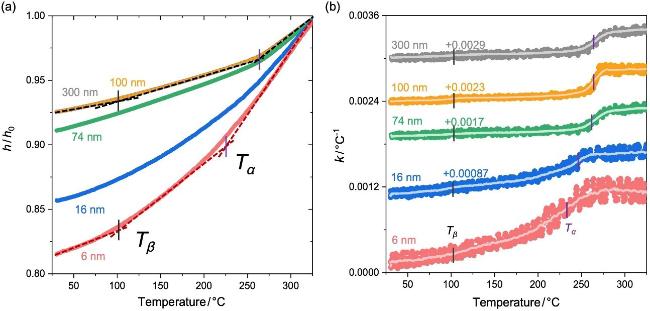
椭圆偏振光谱对薄膜厚度的测定具有亚纳米级的超高分辨率, 故可以将此法用于研究厚度低于100 nm的超薄膜松弛行为, 从而弥补DMA或BDS等常规动力学方法难以测量纳米薄膜的局限.
图6a为变温椭圆偏振光谱测量的不同厚度PI薄膜的热膨胀行为. 当薄膜厚度大于100 nm时, 聚酰亚胺膜表现出相同的热膨胀行为; 100 nm和300 nm聚酰亚胺膜的h/h0~T完全重合. 当膜厚降低到74 nm左右时, 薄膜热膨胀行为开始偏离厚膜: 随着膜厚降低, 薄膜的热膨胀变得更显著. 对于6 nm厚度的PI超薄膜, 可以观察到h/h0~T曲线斜率发生了两次转变, 对应着α和β两个松弛转变. 这也说明椭圆偏振光谱是研究超薄膜动态松弛过程的有效方法.
图6 PI薄膜的(a)归一化厚度(h/h0, h0为薄膜在330 ℃下的膜厚)和(b)膨胀系数随温度的变化. 图(b)中的曲线经过纵向平移, 以更好地展示其差异

Figure 6 (a) Normalized thickness (h/h0, h0 is the thickness of films at 330 ℃) and (b) thermal expansion coefficient as a function of temperature for polyimide ultrathin films. The curves in panel (b) have been vertically shifted for better presentation of their difference

图6b为不同厚度PI薄膜的k与温度的依赖性. 随着PI薄膜的膜厚降低, Tα明显降低, 转变的温度区域增宽; 而β松弛温度Tβ几乎不发生变化. 图7a总结了PI薄膜Tβ与Tα与薄膜厚度的关系. 结果表明, 当膜厚大于约100 nm时, 薄膜的Tα不随膜厚而变化; 继续降低膜厚, Tα随着薄膜厚度的降低而减小. 这表明纳米受限加速了PI薄膜的链段松弛. 然而, PI薄膜的Tβ却不随膜厚的变化而改变. 薄膜Tα的纳米受限效应来源于自由表面的作用. 自由表面附近的链段缺少周围分子链段的相互作用, 协同性与耦合作用减弱, 运动加快; 随着膜厚降低, 快的表面链段贡献增加从而加速薄膜的松弛, 使Tα降低[53-55]. 而β松弛仅涉及局部的基团运动, 不参与链段间的协同与耦合[55-56]; 因此, β松弛不受自由表面所带来的链段运动耦合性改变的影响, Tβ不表现出膜厚依赖性[57].
图7 PI超薄膜的(a) Tα, Tβ及(b) k的膜厚依赖性

Figure 7 Film thickness dependence of (a) Tα, Tβ and (b) k for polyimide ultrathin films

图7b还总结了PI薄膜k1, k2和k3与膜厚的关系. 结果表明, 随着膜厚降低, PI的热膨胀更加剧烈, k1, k2与k3均呈增加的趋势. 膨胀系数增大降低了纳米薄膜的热稳定性[58], 增加了薄膜各类物理性质的热敏感性, 对于PI薄膜作为热管理材料、芯片封装材料的应用产生不利影响.

3 结论与展望

本工作制备了从微米级到纳米级的芳香型BPDA-ODA聚酰亚胺薄膜, 利用宽频介电谱、动态力学分析以及变温椭圆偏振光谱研究了PI本体和纳米薄膜的多级松弛行为. 结果表明PI在270和100 ℃附近分别出现链段运动的α松弛和芳香环转动的β松弛过程. 并且, 随着PI薄膜厚度降低至100 nm, PI的α转变温度 (Tα)降低, 而β转变温度(Tβ)基本不变, 热膨胀系数显著增大. 这一结果说明PI薄膜的多级松弛行为存在不同的膜厚依赖性. 该结果对于PI薄膜的应用具有重要意义. 一方面, PI超薄膜升高的膨胀系数降低了薄膜热稳定性, 可能在薄膜与器件界面产生热应力, 造成薄膜剥离甚至引起器件翘曲和断裂. 另一方面, 纳米PI薄膜降低的Tg可能加速薄膜在使用过程中发生物理老化, 从而使得薄膜变脆、表面产生银纹等, 造成器件失效. 因此, 开发具有低热膨胀系数和高Tg的高稳定PI超薄膜对于精密器件的设计和制备至关重要. 如何调控纳米PI薄膜的松弛和热转变行为, 抑制薄膜热膨胀将是未来PI薄膜研究的重要方向.

4 实验部分

4.1 材料

联苯四甲酸二酐(biphenyltetracarboxylic diand- hydride, BPDA, AR)、4,4'-二氨基二苯醚(4,4'-oxydi- aniline, ODA, AR)、N,N-二甲基乙酰胺(N,N-dimethyl-acetamide, DMAc)、甲醇(AR)均购自上海麦克林生化科技股份有限公司, 直接使用.

4.2 聚酰胺酸(Polyamide Acid, PAA)膜的制备

利用两步法制备BPDA-ODA型聚酰亚胺薄膜(图1). 首先是聚酰胺酸(PAA)溶液的合成: 氮气保护下, 在250 mL三口玻璃中将30.0 mmol的ODA溶解于120 mL的DMAc形成均相溶液. 利用冰水浴将反应体系温度控制在0 ℃附近, 向溶液中一次性加入28.0 mmol的BPDA粉末, 搅拌至完全溶解后再加入20 mL DMAc并持续反应2~3 h. 最后, 再分批加入2.0 mmol的BPDA以调节聚合度, 获得粘稠的PAA/DMAc溶液. 利用甲醇沉淀产物, 并将其再次溶解于DMAc, 反复多次纯化上述产物以除去未反应单体, 得到淡青色的PAA固体.
利用浇铸法和旋涂法(Spin-coating)制备不同厚度聚酰胺酸(PAA)薄膜: 制备微米级PAA膜时采用浇铸成膜法, 将PAA溶液(20% (w))均匀涂覆在洁净的玻璃板上, 在洁净工作台放置24 h待溶剂自然挥发成膜; 制备纳米级PAA超薄膜时采用旋涂成膜法, 将PAA溶液涂覆于硅片表面, 以3000 r/min转速旋涂20 s, 通过调节PAA溶液浓度得到不同厚度PAA纳米超薄膜.

4.3 PAA膜高温亚胺化制备聚酰亚胺薄膜

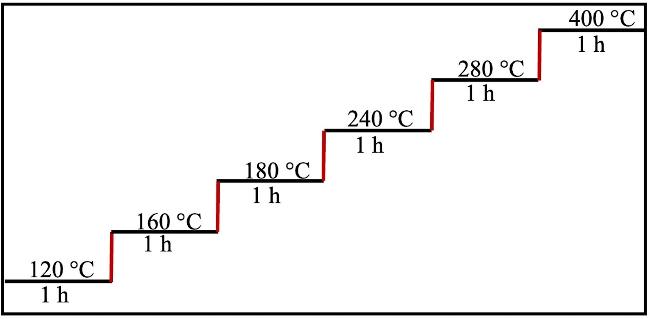
通过PAA薄膜的高温亚胺化制备聚酰亚胺薄膜: 将PAA膜放入程序控温的真空烘箱中进行亚胺化, 具体的升温程序见图8. 高温亚胺化后, 得到厚度约为80 μm的平整PI浇铸膜以及不同厚度(6~300 nm)的PI纳米超薄膜. 高温亚胺化前后, 薄膜表面保持平整, 它们的表面形貌见图9中的原子力显微镜(AFM)照片, 表面粗糙度(Ra)均小于0.2 nm.
图8 PAA薄膜高温亚胺化制备PI薄膜的升温程序图

Figure 8 Temperature protocol for preparing PI films by imidization of PAA films at high temperature

图9 (a) 20 nm PAA薄膜及其(b)经过高温亚胺化后得到的PI超薄膜表面形貌的AFM图

Figure 9 AFM morphological images of (a) 20 nm PAA film and (b) the corresponding PI films by imidization

4.4 表征方法

核磁共振氢谱(1H NMR): 采用德国Bruker公司的AVANCEII/400型核磁共振波谱仪进行测试, 溶剂采用氘代二甲基亚砜(DMSO-d6, 溶剂峰化学位移为2.50).
全反射傅里叶变换红外光谱(ATR FT-IR): 使用美国ThermoFisher Scientific公司的Nicolet 5700型红外光谱仪进行测试, 波数扫描范围为500~4000 cm−1, 扫描次数为32次.
宽频介电谱(BDS): 采用德国Novocontrol公司Concept 50型介电谱仪进行测试, 测试温度范围为150~330 ℃, 每间隔20 ℃进行等温扫频测试, 频率范围10−1~107 Hz.
动态力学分析(DMA): 使用瑞士Mettler Toledo公司的DMA1型动态力学分析仪, 以速率3 ℃/min在30~330 ℃温度范围内进行线性升温测试. PI膜裁剪成40 mm×5 mm×80 μm的片状样条. 测试采用拉伸模式, 样条的有效拉伸长度为30 mm; 控制测试的正弦拉伸幅度为10 μm (应变振幅为0.03%), 正弦频率分别为fDMA=0.2, 1及3 Hz.
变温椭圆偏振光谱: 采用美国J. A. Woollam公司的M-2000V型椭圆偏振光谱仪进行测试, 波长(λ)覆盖350~1500 nm. 实验中, 使用英国Linkam公司的热台对薄膜样片进行控温, 分别以q=5, 10及20 ℃/min的速率在30~330 ℃的范围进行线性升温. 同时, 利用椭圆偏振光谱仪原位测定薄膜的光谱Ψ(λ)和Δ(λ); 其中Ψ(λ)和Δ(λ)分别是经薄膜反射后, 两个偏振分量的入射光线和反射光线之间的振幅改变和相位改变. 椭圆偏振光谱Ψ(λ)和Δ(λ)经过光学模型的拟合处理可以给出薄膜的厚度(h), 其厚度分辨率精确到0.1 nm.
原子力显微镜(AFM): 使用美国Bruker公司的ICON Fastscan型原子力显微镜. 测试采用轻敲模式(tapping mode); 扫描结果使用NanoScope Analysis软件进行处理和分析.
(Cheng, B.)

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Ding, M. Polyimide—Chemistry, Structure-Property Relationships, and Materials, Second Edition, Science Press, Beijing, 2012 (in Chinese).

(丁孟贤, 聚酰亚胺—化学、结构与性能的关系及材料, 第二版, 科学出版社, 北京, 2012.)

[2]
Khan, A. I.; Daus, A.; Islam, R.; Neilson, K. M.; Lee, H. R.; Wong, H. S. P.; Pop, E. Science 2021, 373, 1243.

[3]
Liu, J.; Ni, H.; Gao, H.; Yang, S. Spacecraft Environm. Eng. 2014, 31, 470 (in Chinese).

(刘金刚, 倪洪江, 高鸿, 杨士勇, 航天器环境工程, 2014, 31, 470.)

[4]
Ni, H.; Liu, J.; Wang, Z.; Yang, S. J. Ind. Eng. Chem. 2015, 28, 16.

[5]
Dong, J.; Li, L.; Niu, Y.; Pan, Z.; Pan, Y.; Sun, L.; Tan, L.; Liu, Y.; Xu, X.; Guo, X.; Wang, Q.; Wang, H. Adv. Energy Mater. 2024, 14, 2303732.

[6]
Niu, H.; Bai, X.; Huang, Y.; Wang, C. Acta Chim. Sinica 2005, 63, 1391 (in Chinese).

(牛海军, 白续铎, 黄玉东, 汪成, 化学学报, 2005, 63, 1391.)

[7]
Yang, J.; Zhan, H.; Zhou, X.; Hu, J.; Liu, Y.; Gu, Y.; Liu, X. Acta Chim. Sinica 2009, 67, 875 (in Chinese).

(杨进, 詹怀宇, 周雪松, 胡健, 刘辕, 顾宜, 刘向阳, 化学学报, 2009, 67, 875.)

[8]
Yu, Q.; Zhu, L.; Liu, T.; Babu, S. S.; Zheng, Z.; Liu, S.; Chi, Z.; Zhang, Y.; Xu, J. Adv. Mater. Interfaces 2021, 8, 2001786.

[9]
Fan, Z.; Liu, S.; Chi, Z.; Zhang, Y.; Xu, J. Acta Polym. Sin. 2021, 52, 750 (in Chinese).

(范振国, 刘四委, 池振国, 张艺, 许家瑞, 高分子学报, 2021, 52, 750.)

[10]
Nimbalkar, P.; Bhaskar, P.; Kathaperumal, M.; Swaminathan, M.; Tummala, R. R. Polymers 2023, 15, 3895.

[11]
Soles, C. L.; Ding, Y. Science 2008, 322, 689.

[12]
Luo, J.; Xu, Q.; Xu, W.; Zuo, B. Acta Polym. Sin. 2025, 56, 539 (in Chinese).

(罗锦添, 徐全印, 徐文生, 左彪, 高分子学报, 2025, 56, 539.)

[13]
Tian, H.; Xu, Q.; Zhang, H.; Priestley, R. D.; Zuo, B. Appl. Phys. Rev. 2022, 9, 011316.

[14]
Yang, Y.; Tian, H.; Napolitano, S.; Zuo, B. Prog. Polym. Sci. 2023, 144, 101725.

[15]
Chen, Y.; Zhou, D.; Hu, W. Acta Polym. Sin. 2021, 52, 423 (in Chinese).

(陈咏萱, 周东山, 胡文兵, 高分子学报, 2021, 52, 423.)

[16]
Keddie, J. L.; Jones, R. A. L.; Cory, R. A. Europhys. Lett. 1994, 27, 59.

[17]
Forrest, J. A.; Dalnoki-Veress, K. Adv. Colloid Interface Sci. 2001, 94, 167.

[18]
Fukao, K.; Miyamoto, Y. Phys. Rev. E 2000, 61, 1743.

PMID

[19]
Roth, C. B.; Dutcher, J. R. J. Electroanal. Chem. 2005, 584, 13.

[20]
Yang, Z.; Fujii, Y.; Lee, F. K.; Lam, C.-H.; Tsui, O. K. C. Science 2010, 328, 1676.

[21]
Yang, Y.; Shen, H.; Zuo, B. Huaxue Tongbao 2024, 87, 258 (in Chinese).

(阳禹辉, 沈华琦, 左彪, 化学通报, 2024, 87, 258.)

[22]
Reiter, G. Macromolecules 1994, 27, 3046.

[23]
Luo, J.; Zha, H.; Tian, H.; Zuo, B. Chin. J. Polym. Sci. 2024, 43, 1163.

[24]
Wang, Q.; Wang, W.; Wu, C.; Luo, J.; Zhou, J.; Zuo, B. Macromolecules 2024, 57, 10112.

[25]
Xu, Q.; Zhu, N.; Fang, H.; Wang, X.; Priestley, R. D.; Zuo, B. ACS Macro Lett. 2021, 10, 1.

[26]
Richard, A. L. Faraday Discuss. 1994, 98, 219.

[27]
Tian, H.; Luo, J.; Tang, Q.; Zha, H.; Priestley, R. D.; Hu, W.; Zuo, B. Nat. Commun. 2024, 15, 6082.

[28]
Serghei, A.; Tress, M.; Kremer, F. Macromolecules 2006, 39, 9385.

[29]
Wang, T.; Pearson, A. J.; Dunbar, A. D. F.; Staniec, P. A.; Watters, D. C.; Coles, D.; Yi, H.; Iraqi, A.; Lidzey, D. G.; Jones, R. A. L. Eur. Phys. J. E 2012, 35, 129.

[30]
Liu, D.; Qin, H.; Zhang, J.; Wang, T. Phys. Rev. E 2016, 94, 052503.

[31]
Campoy-Quiles, M.; Sims, M.; Etchegoin, P. G.; Bradley, D. D. C. Macromolecules 2006, 39, 7673.

[32]
Gomopoulos, N.; Saini, G.; Efremov, M.; Nealey, P. F.; Nelson, K.; Fytas, G. Macromolecules 2010, 43, 1551.

[33]
Bai, F.; Jiang, Y.; Li, X.; Dong, J.; Zhao, X.; Zhang, Q. Acta Polym. Sin. 2024, 55, 1393 (in Chinese).

(白帆, 江怡雯, 李琇廷, 董杰, 赵昕, 张清华, 高分子学报, 2024, 55, 1393.)

[34]
Kim, Y. H.; Moon, B. S.; Harris, F. W.; Cheng, S. Z. D. J. Therm. Anal. 1996, 46, 921.

[35]
Comer, A. C.; Kalika, D. S.; Rowe, B. W.; Freeman, B. D.; Paul, D. R. Polymer 2009, 50, 891.

[36]
Khazaka, R.; Locatelli, M. L.; Diaham, S.; Bidan, P.; Dupuy, L.; Grosset, G. J. Phys. D: Appl. Phys. 2013, 46, 065501.

[37]
Lunkenheimer, P.; Loidl, A.; Riechers, B.; Zaccone, A.; Samwer, K. Nat. Phys. 2023, 19, 694.

[38]
Luo, P.; Wolf, S. E.; Govind, S.; Stephens, R. B.; Kim, D. H.; Chen, C. Y.; Nguyen, T.; Wąsik, P.; Zhernenkov, M.; McClimon, B.; Fakhraai, Z. Nat. Mater. 2024, 23, 688.

[39]
Luo, J.; Ye, K.; Li, J.; Zuo, B. Rev. Sci. Instrum. 2025, 96, 053904.

[40]
Ding, Y.; Bikson, B.; Nelson, J. K. Macromolecules 2002, 35, 912.

[41]
Ni, H.; Xing, Y.; Dai, X.; Li, J.; Zhang, D.; Yang, S.-Y.; Chen, X.-B. J. Mater. 2019, 47, 100.

[42]
Wang, C.; Zhao, H.; Li, G.; Jiang, J. Acta Chim. Sinica 2010, 68, 449 (in Chinese).

(汪称意, 赵辉鹏, 李光, 江建明, 化学学报, 2010, 68, 449.)

[43]
Huang, W.; Yan, D.; Lu, Q. Chem. J. Chinese U. 2002, 23, 2005 (in Chinese).

(黄卫, 颜德岳, 路庆华, 高等学校化学学报, 2002, 23, 2005.)

[44]
Zhao, L.; Huang, Y.; Piao, Y.; Meng, X.; Song, Y.; Long, J. Acta Chim. Sinica 2009, 67, 1013 (in Chinese).

(赵亮, 黄玉东, 朴艳梅, 孟祥丽, 宋元军, 龙军, 化学学报, 2009, 67, 1013.)

[45]
Wang, X.; Li, Y.-F.; Ma, T.; Zhang, S.; Gong, C. Polymer 2006, 47, 3774.

[46]
Havriliak, S.; Negami, S. Polymer 1967, 8, 161.

[47]
Fulcher, G. S. J. Am. Ceram. Soc. 1925, 8, 339.

[48]
Tammann, G.; Hesse, W. Z. Anorg. Allg. Chem. 1926, 156, 245.

[49]
Luo, J.; Wang, X.; Tong, B.; Li, Z.; Rocchi, L. A.; Di Lisio, V.; Cangialosi, D.; Zuo, B. J. Phys. Chem. Lett. 2024, 15, 357.

[50]
Wang, F.; Sun, P. Acta Polym. Sin. 2021, 52, 840 (in Chinese).

(王粉粉, 孙平川, 高分子学报, 2021, 52, 840.)

[51]
Yuan, Q.; Yang, Z.; Xu, W. Sci. Sin. Chim. 2023, 53, 616 (in Chinese).

(袁琦璐, 杨镇岳, 徐文生, 中国科学(化学), 2023, 53, 616.)

[52]
Zhang, Q.; Luo, W.; Gao, L.; Chen, D.; Ding, M. J. Appl. Polym. Sci. 2004, 92, 1653.

[53]
Salez, T.; Salez, J.; Dalnoki-Veress, K.; Raphaël, E.; Forrest, J. A. Proc. Natl. Acad. Sci. 2015, 112, 8227.

[54]
Ngai, K. L.; Rizos, A. K.; Plazek, D. J. J. Non-Cryst. Solids 1998, 235-237, 435.

[55]
Ngai, K. L.; Paluch, M.; Rodríguez-Tinoco, C. Phys. Chem. Chem. Phys. 2017, 19, 29905.

DOI PMID

[56]
Ngai, K. L.; Paluch, M. J. Chem. Phys. 2004, 120, 857.

PMID

[57]
Hartmann, L.; Gorbatschow, W.; Hauwede, J.; Kremer, F. Eur. Phys. J. E 2002, 8, 145.

[58]
Wang, C.; Zhai, L.; Gao, M.; Jia, Y.; Mo, S.; He, M.; Fan, L. Sci. Sin. Chim. 2022, 52, 437 (in Chinese).

(王畅鸥, 翟磊, 高梦岩, 贾妍, 莫松, 何民辉, 范琳, 中国科学, 2022, 52, 437.)

Options
Outlines

/

〈 〉