1 引言
在自然环境中, 硼元素的存在形态多种多样[1-7]. 其中, 硼团簇由于多样的几何构型以及特殊的成键性质成为研究焦点. 典型的硼团簇结构涵盖了平面(例如${B}_{8}^{-}$和${B}_{9}^{-}$)[4]、管状[8]、笼状(例如阴离子${B}_{40}^{-}$和中性B40, 也称作硼球烯)[2]以及核-壳双层结构(如B48)[9-10]等. 通常而言, 较小尺寸的硼团簇倾向于形成平面或准平面几何构型[4,6,11-13], 其稳定性主要源于平面内离域σ键和π键的共同作用[4,6-7]. 近年来, 结合光电子能谱(PES)与理论计算研究报道了一系列阴离子硼团簇[14-17]. 其中小分子硼团簇${B}_{7}^{3-}$、${B}_{8}^{2-}$和${B}_{9}^{-}$具有相同的特点: 均包含一个中心硼原子与一个单环分子. 深入分析表明, 具有C6v对称性的${B}_{7}^{3-}$、D7h对称性的${B}_{8}^{2-}$以及D8h对称性的${B}_{9}^{-}$均为双重芳香性配体, 具有6个离域σ电子和6个离域π电子. 值得注意的是, 它们的成键特征分别与环戊二烯负离子(${\text{C}}_{5}^{}{H}_{5}^{-}$)、苯(C6H6)和环庚三烯正离子(${\text{C}}_{7}^{}{H}_{7}^{+}$)具有相似性, 因此被统称为“borozenes”[18].
硼团簇的结构和性质可以通过掺杂金属原子进一步调整, 根据掺杂金属原子的数量, 可划分为单金属掺杂与多金属掺杂两大类别. 单金属掺杂体系以过渡金属为代表, 包括平面构型的Co©B₈、Ru©B₉[12]、Ta©B₁₀与Nb©B₁₀[19], 其中$Au{B}_{10}^{-}$已通过PES表征[20]. 此外, 碱金属[21-22]、碱土金属[23-24]以及镧系(Ln)和锕系(An)元素亦可掺杂到硼团簇中. 在对基于${B}_{8}^{2-}$团簇的borozene配合物的研究中[25-29], 首例报道的配合物是$Al{B}_{8}^{-}$[27], 呈现C7v对称性, 中性体系AlB8也是具有C7v结构的配合物. 不同金属掺杂的${B}_{8}^{2-}$体系的结构具有多样性, 例如, 当Au和Bi掺杂${B}_{8}^{2-}$时, 金属位于硼环边缘附近[25,30]. PbB8簇是具有C7v半夹心结构的配合物. 通过PES和理论研究发现, 另一种配合物$Cu{B}_{8}^{-}$具有高稳定性, 也具有半夹心结构. 镧系元素掺杂的硼团簇$Ln{B}_{8}^{-}$(Ln=La, Pr, Tb, Tm, Yb)已通过PES和理论计算进行了研究. 从轻稀土元素到重稀土元素, $Ln{B}_{8}^{-}$的全局最小结构从Cs变为C7v, 并且C7v结构中镧系元素为低价Ln(I)[31]. 我们通过全局最优结构搜索和密度泛函理论(DFT)研究了一系列以${B}_{7}^{3-}$为配体的锕系配合物AnB7 (An=Pa~Pu)[32], 发现这些配合物中锕系元素都为＋3价. 最近, Li和Burkhardt对锕系硼团簇$An{B}_{8}^{-}$(An=Ac、Pa、Bk、Md和No)[33]进行了理论研究, 发现半夹心结构的配合物锕系元素的氧化态为＋I.
相对于其他borozene配合物, 目前对锕系相关配合物的研究非常有限. 我们之前预测了一系列锕系配合物AnB8 (An=Pa~Pu), 为AnII[${B}_{8}^{2-}$]型配合物[34]. 考虑到所掺杂金属原子的尺寸可能会影响硼团簇的结构和性质, 我们选择原子半径较大的Ac、Th、Am和Cm锕系金属作为掺杂原子, 通过全局最优结构搜索和DFT系统研究了一系列AnB8 (An=Ac, Th, Am, Cm)团簇. 研究发现, 这些硼团簇为稳定的二价锕系配合物. 本工作有望为设计低价锕系元素配合物提供理论参考.
2 结果与讨论
2.1 AnB8的结构
对于ThB8, 基于全局结构搜索的结果, 在PBE0/6-311＋G*/RECP和TPSSH/6-311＋G*/RECP理论水平下优化了前五种能量较低异构体的结构, 其中半夹心结构能量最低, 椅状构型次之(图1). 考虑到Ac、Am和Cm的原子半径与Th的原子半径接近, 基于ThB8的两种能量较低异构体(半夹心和椅状构型), 分别优化了AcB8、AmB8和CmB8的结构. 对于每种异构体, 在PBE0/6-311＋G*/RECP和TPSSH/6-311＋G*/RECP理论水平下考虑了不同的自旋态: AcB8考虑了双重态, ThB8计算了单重态和三重态, 对于AmB8则考虑了双重态、四重态、六重态和八重态, CmB8考虑了单重态、三重态、五重态、七重态和九重态. 各自旋态的相对能量列于支持信息表S1, 图1为优化后的AnB8结构.
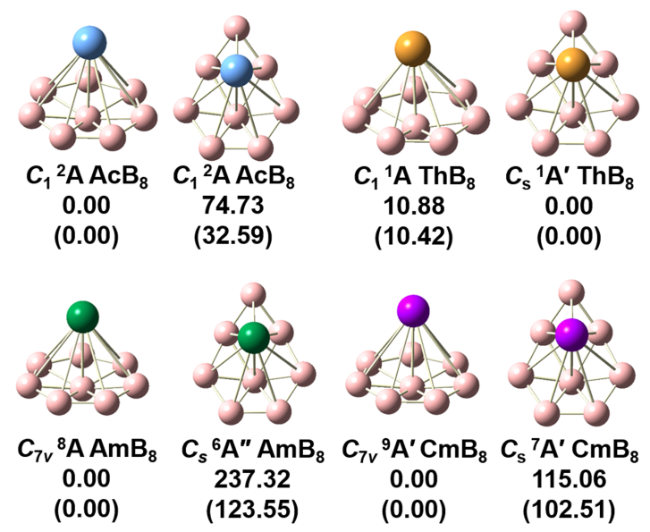
图1 在PBE0/6-311＋G*/RECP理论水平下优化得到的AnB8结构以及相对能量(括号内为TPSSH方法计算的相对能量, kJ/mol). 粉色球体代表B原子, 蓝色球体代表Ac原子, 橙色球体代表Th原子, 绿色球体代表Am原子以及紫色球体代表Cm原子Figure 1 The optimized geometrical structures and relative energies of AnB8 at the PBE0/6-311＋G*/RECP level of theory (The brackets represent the relative energies calculated by the TPSSH method, kJ/mol). The pink spheres represent the B atom, the blue, orange, green, and purple spheres represent the Ac, Th, Am, and Cm atoms, respectively |
如图1所示, 对于AcB8, 半夹心结构比椅状结构的能量低74.73 kJ/mol (PBE0)或32.59 kJ/mol (TPSSh), AmB8和CmB8的半夹心结构也较为稳定, 且为C7v对称性. AcB8、AmB8和CmB8的双重态、八重态和九重态结构更稳定. ThB8的椅状结构更稳定, 且为单重态结构, 但其与半夹心结构的能量差异较小, 仅为10.88 kJ/mol (PBE0)或10.42 kJ/mol (TPSSh), 在实验中这两种异构体可能会共同存在. 在后续的分析中, 我们只讨论具有半夹心结构的AnB8团簇. 为评估AnB8的多参考特征, 采用CCSD(T)/cc-pVTZ/RECP方法对AnB8的半夹心结构进行单点计算. 计算得到的CCSD T1诊断值小于0.03(见支持信息表S2), 表明这些结构没有显著的多参考特征[35-37].
表1 在PBE0/6-311＋G*/RECP理论水平下计算的AnB8自旋态、自旋污染计算值与理论值的差值⟨S2⟩计算值-理论值、Mulliken原子自旋密度(ρAn)以及An—B1和An—Ba键的平均键长(B1原子为中心的硼原子, 而Ba原子为硼环上的硼原子)Table 1 Spin states, the differences between the calculated and theoretical spin contamination ⟨S2⟩计算值-理论值, Mulliken atomic spin densities (ρAn), and average An—B1 and An—Ba average bond distances (the B1 atom is the central boron atom of the boron ring, while the Ba atoms are the peripheral boron atoms of the boron ring) for AnB8 at the PBE0/6-311＋G*/RECP level of theory |
| 硼团簇 | 自旋态 | ⟨S2⟩计算值-理论值 | 自旋密度 ρAn | 键长/nm | |
|---|---|---|---|---|---|
| An—B1 | An—Ba | ||||
| AcB8 | 双重态 | 0.00 | 0.77 | 0.2750 | 0.3017 |
| ThB8 | 单重态 | — | — | 0.2485 | 0.2729 |
| AmB8 | 八重态 | 0.02 | 7.14 | 0.2573 | 0.2882 |
| CmB8 | 九重态 | 0.03 | 8.10 | 0.2588 | 0.2849 |
对于AnB8的半夹心结构, 计算得到An—B1 (B1为中心的硼原子)的键长为0.2485至0.2750 nm, 与An和B的相应单键共价半径之和相近[40]. 在每种AnB8体系中, An—Ba (Ba为硼环上的硼原子)键的平均键长明显长于An—B1键(0.2729~0.3017 nm), 表明其相互作用较弱.
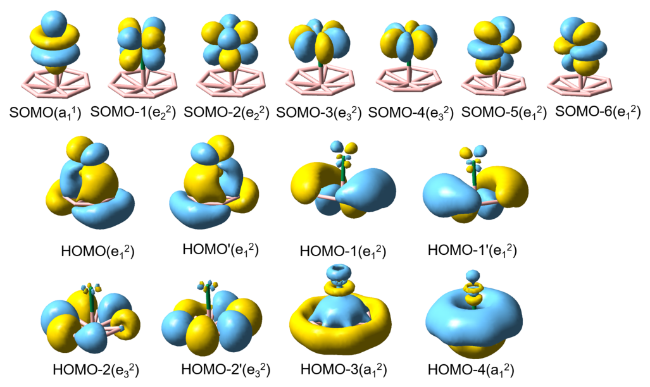
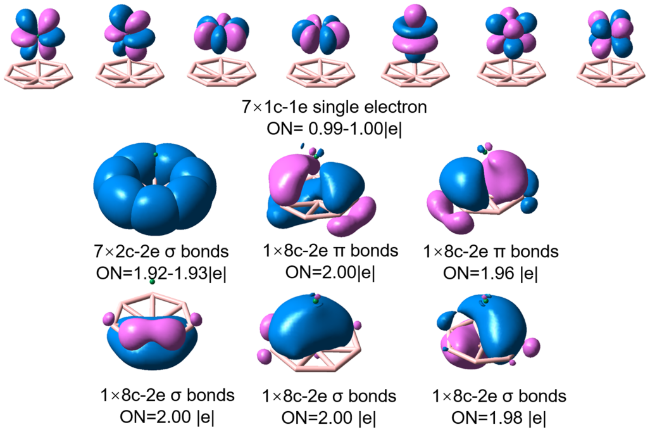
2.2 AnB8的成键性质
在相同理论水平下, 计算了AnB8的Voronoi变形密度(VDD)电荷[41]和Hirshfeld电荷[42], 以评估配合物中锕系离子和${B}_{8}^{2-}$配体之间的电荷转移. 这些电荷是通过对形成化学键时流入和流出原子的电子密度数进行空间积分来计算的. VDD电荷分析不受基组的影响, 主要用于计算特定原子或碎片之间的电荷流. Hirshfeld电荷的计算速度更快, 并且不依赖于计算所使用的基组. 由于锕系元素的电负性低于硼原子的电负性, 因此电荷从锕系元素流向硼配体. 如表2所示, 锕系金属原子的VDD电荷值均为正值, 范围为0.607至0.766, 其中AmB8的电荷最高. 对于Hirshfeld电荷, AnB8的电荷在0.636和0.807之间, 同样AmB8的电荷最高. 这些结果表明, AmB8中的电荷转移小于其他配合物中的电荷转移. AnB8中发生的电荷重排可能受到锕系金属阳离子和${B}_{8}^{2-}$配体之间的成键相互作用的影响. An—B1键的Wiberg键级(WBIs)值在0.346 (AmB8)到0.516 (ThB8)之间, 其中AmB8的WBIs值最小, 而ThB8的WBIs值最大, 表明Th—B1键的共价相互作用更强. 对于每个配合物, An原子和外周Ba原子(An—Ba键)的WBIs小于 An—B1键的相应值, 与较长的An—Ba键长一致, 表明在半夹心结构中, An原子和B1原子之间的相互作用比Ba原子更强.
表2 在PBE0/6-311＋G*/RECP理论水平下, 计算得到的AnB8体系An的电荷、An—B键的WBI以及AnB8的SOMO-LUMO能隙(eV)Table 2 The charge analysis of An, WBIs of the An-B bonds, and the SOMO-LUMO gap (eV) of AnB8 at the PBE0/6-311＋G*/RECP level of theory |
| 硼团簇 | 原子电荷/a.u. | WBIs | SOMO-LUMO 能隙/eV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| VDD | Hirshfeld | An—B1 | An—Ba | α | β | |||||
| AcB8 | 0.743 | 0.796 | 0.620 | 0.421 | 1.20 | 3.45 | ||||
| ThB8 | 0.746 | 0.723 | 0.611 | 0.516 | 1.49 | — | ||||
| AmB8 | 0.766 | 0.807 | 0.638 | 0.346 | 2.91 | 3.50 | ||||
| CmB8 | 0.607 | 0.636 | 0.631 | 0.425 | 2.16 | 3.81 | ||||
由于分子中原子的量子理论(QTAIM)[43]不依赖基组, 直接基于电子密度提供定量的化学键分析, 因此在PBE0/6-311＋G*/RECP理论水平下, 对AnB8进行了QTAIM分析. 在此分析中, 能量密度(H)、电子密度(ρ)和拉普拉斯电子密度(∇2ρ)用于描述两个原子之间键临界点(BCP)的成键特性. 如图2所示, ThB8显示四个 Th—B BCPs, 包括一个Th—B1和三个Th—Ba键. 在AcB8、AmB8和CmB8中, 仅发现一个An—B1 BCP. 这些An—B BCPs表明AnB8中存在金属-硼之间的相互作用. 表3列出了在An—B BCPs处计算的ρ、∇2ρ和H值. 如表3所示, 所有ρ值低于0.1 a.u., 介于0.039和0.062 a.u.之间, ∇2ρ值范围为0.0665至0.11792 a.u., 表明An—B键主要为离子键. H值均为负值, 范围从 －0.00726到－0.01692 a.u., 表明这些An—B键存在部分共价特征.
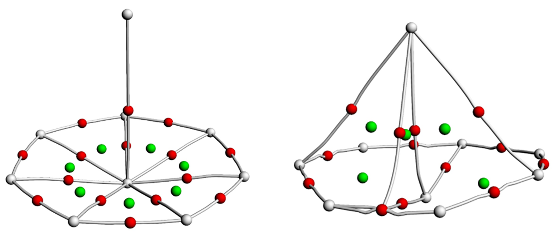
图2 在PBE0/6-311＋G*/RECP理论水平下, AcB8、AmB8、CmB8(左)和ThB8(右)的QTAIM分析. 红点代表键临界点, 灰线代表键路径, 绿点代表环临界点Figure 2 The QTAIM analysis of AcB8, AmB8, CmB8 (left) and ThB8 (right) at the PBE0/6-311＋G*/RECP level of theory. Red points represent bond critical points, grey lines represent bond paths, and green points represent ring critical points |
表3 在PBE0/6-311＋G*/RECP理论水平下AnB8的QTAIM分析(a.u.)Table 3 The QTAIM analysis (a.u.) of AnB8 at the PBE0/6-311＋G*/RECP level of theory |
| 硼团簇 | ρ | H | ∇2ρ | ELF | DItotal |
|---|---|---|---|---|---|
| AcB8 | 0.03987 | －0.00481 | 0.07581 | 0.24085 | 2.387 |
| ThB8 | 0.06165 | －0.01692 | 0.06650 | 0.40489 | 3.628 |
| AmB8 | 0.04167 | －0.00736 | 0.11279 | 0.14418 | 1.800 |
| CmB8 | 0.04180 | －0.00726 | 0.11792 | 0.13616 | 2.226 |
以AmB8为代表, 采用PBE0方法对配合物进行了Kohn-Sham分子轨道(MO)分析, 结果如图3所示. AmB8为开壳层电子构型, 具有七个SOMO轨道, 主要为锕系元素的5f轨道. 根据MO分析, AmB8配合物的HOMO(2e12)和HOMOʹ(2e12)轨道为Am—B成键轨道, 主要来自Am的5f(63.8%)轨道与硼原子的2p轨道之间的相互作用. 其他轨道为配体硼环内的离域轨道, 主要来源于B的2p轨道. 在AmB8中, HOMO-1(1e12)、HOMO-1ʹ(1e12)和HOMO-4(1a12)为离域π键轨道, 而HOMO(2e12)、HOMOʹ(2e12)和HOMO-3(2a12)属于离域键σ轨道, 如图3所示. 此外, 计算得到的AmB8中${B}_{8}^{2-}$的核独立化学位移NICS(0)_ZZ和NICS(1)_ZZ值均为负值, 分别为－389.2和－204.2. 因此, AnB8配合物中${B}_{8}^{2-}$配体具有双重芳香性, 这与AnB8 (An=Pa~Pu)一致[34].
对于其他AnB8配合物, 也同样存在An—B成键轨道(见支持信息图S1). 如图S1所示, 在AcB8和ThB8的An—B成键轨道中, 主要为An的6d轨道参与成键, 而对于AmB8和CmB8, An的5f轨道为主要贡献. 因此由AcB8、ThB8到AmB8、CmB8, An—B成键轨道中, An的6d轨道特征逐渐减弱, 5f轨道特征则有所增强.
2.3 AnB8的热力学稳定性
在PBE0/6-311＋G*/RECP理论水平下, 通过AnB8→An2＋＋${B}_{8}^{2-}$反应计算AnB8的解离能(DE), 评估其热力学稳定性. 其中, ${B}_{8}^{2-}$的结构也在PBE0/6-311＋G*/RECP理论水平下进行了优化, 其具有平面结构. 如表4所示, 这些解离反应的DE值都为正值, 且相对较大, 表明这些二价锕系配合物具有较高的热力学稳定性. 因此, ${B}_{8}^{2-}$配体能够稳定二价锕系元素. ThB8的DE值为2384.0 kJ/mol, 在AnB8体系中最高. 这与ThB8具有更强的Th—B共价键一致. AmB8在AnB8体系中显示出最低的DE值(1988.2 kJ/mol), 这与An—B键共价相互作用的趋势一致, 表明共价相互作用是决定这些配合物之间相对稳定性的主要因素.
表4 在PBE0/6-311＋G*/RECP理论水平下计算的AnB8的解离能(kJ/mol)Table 4 The dissociation energy (kJ/mol) of AnB8 at the PBE0/6-311＋G*/RECP level of theory |
| 反应方程 | 解离能 |
|---|---|
| AcB8→Ac2＋＋${B}_{8}^{2-}$ | 2055.6 |
| ThB8→Th2＋＋${B}_{8}^{2-}$ | 2384.0 |
| AmB8→Am2＋＋${B}_{8}^{2-}$ | 1988.2 |
| CmB8→Cm2＋＋${B}_{8}^{2-}$ | 2190.7 |
2.4 AnB8的模拟红外谱图
对于所有AnB8, 在PBE0/6-311＋G*/RECP理论水平下进行了谐振频率分析并模拟了红外光谱(图5). 为了进行对比分析, 在相同的理论水平下计算了${B}_{8}^{2-}$的红外光谱(见支持信息图S2). AnB8的红外光谱峰主要位于200至1000 cm−1之间, 这些峰的振动模式包括An—B键和B—B键的振动. 模拟的AmB8的红外光谱如图5所示. 其中位于631和978 cm−1处的红外峰对应于硼环的振动, 与${B}_{8}^{2-}$(如图S2)相似, 表现出类似的特征峰(670、975 cm−1). 较低的IR特征峰209 cm−1归因于 An—B之间的振动. 对于CmB8, 硼环的振动峰位于653和987 cm−1处, 而210 cm−1处的特征峰表示Cm—B之间的相互作用. AcB8和ThB8的红外光谱如支持信息图S3所示, 这些体系中也存在相似的特征峰, 表明An—B之间存在直接相互作用.
3 结论
在本工作中, 我们使用全局最优结构搜索和DFT方法系统研究了一系列锕系金属掺杂硼团簇AnB8. 研究表明, 每个AnB8硼团簇都具有两种构型(半夹心和椅状结构), 其中AcB8、AmB8和CmB8的半夹心结构最稳定, 尽管ThB8的椅状结构较为稳定, 但其与半夹心结构能量差异较小. 所有AnB8的半夹心结构为二价锕系配合物AnII[${B}_{8}^{2-}$]. MO分析表明, AcB8、ThB8与AmB8、CmB8都存在An—B成键轨道, 且参与成键的6d轨道贡献逐渐减弱, 而5f轨道特征有所增强. MO和AdNDP分析证实AnB8中An—B之间存在直接的共价相互作用. 其中, ThB8配合物具有更强的金属与配体相互作用. 另外, 所有体系中${B}_{8}^{2-}$为双重芳香性配体. 根据解离能分析, 这些配合物稳定性较高, 其中ThB8较其他配合物更为稳定. ThB8这些不同的性质与其特殊的电子结构有关: 与其他AnB8配合物都为开壳层体系不同, 尽管 Th2＋有两个价电子, 但ThB8为闭壳层单重态体系而不是三重态体系. 本工作有助于提高对锕系金属掺杂硼团簇电子结构的理解, 并为设计低价锕系元素配合物提供理论基础.
4 计算方法
使用结构搜索程序CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization)对ThB8进行全局最小结构搜索[46-49], 评估了1000个结构. 使用VASP (Vienna Ab initio Simulation Package)程序进行了结构弛豫[50-51]. 对于结构优化, 选择PBE0和TPSSh两种方法对结构搜索得到的六种能量较低异构体的结构进行计算, 这两种方法已被证实是计算硼团簇的可靠方法[52-58]. 对于An, 采用ECP60MWB小核赝势和相应的基组ECP60MWB-SEG, B采用6-311＋G*基组进行计算. 基于ThB8的两种能量较低的异构体, 在PBE0/6-311＋G*/RECP和TPSSH/6-311＋G*/RECP理论水平下优化了AcB8、AmB8和CmB8的结构. 同时, 在相同的理论水平下进行了谐振频率计算. 所有结构优化均使用Gaussian 16程序包进行计算[59]. 在PBE0/6-311＋G*/RECP理论水平下, 使用Multiwfn 3.8软件[60-61]获得了Hirshfeld电荷[42]、VDD电荷[41], 另外进行了QTAIM分析[43]、Wiberg键级(WBI)以及UAdNDP[45]分析.
(Cheng, B.)