

含旋轨耦合的耦合簇方法中的基组选择
收稿日期: 2024-03-11
网络出版日期: 2024-04-24
基金资助
国家自然科学基金(22373070); 国家自然科学基金(21973063)
Selection of Basis Sets in Coupled-Cluster Calculations with Spin-Orbit Coupling
Received date: 2024-03-11
Online published: 2024-04-24
Supported by
National Natural Science Foundation of China(22373070); National Natural Science Foundation of China(21973063)
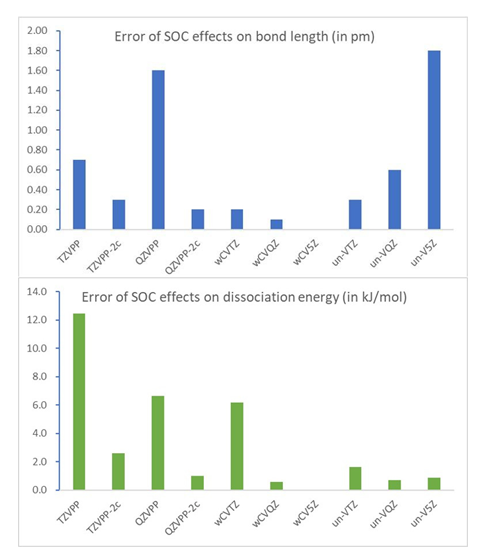
相对论小核能量一致赝势是流行的相对论效应处理方法, 但是除dhf-nZVPP-2c基组外, 针对此赝势开发基组时都没考虑旋轨耦合效应(SOC), 而dhf-nZVPP-2c的可靠性也主要在密度泛函计算中进行了验证. 本工作采用以标量相对论Hartree-Fock波函数为参考态的SOC-CCSD(T)方法结合此类赝势, 考察5s5p电子及各种基函数对第六周期闭壳层双原子分子性质, 特别是SOC效应的影响. 结果显示, 要可靠计算SOC效应, 在SOC-CCSD(T)计算中要考虑5s5p电子. cc-pVnZ-PP基组和dhf-nZVPP基组不能得到可靠的SOC效应, 而dhf-nZVPP-2c和cc-pwCVnZ-PP基组则能合理描述这些体系的SOC效应. 这两套基组对重元素体系性质的误差与相应基组中基函数数目一致, 顺序为: dhf-TZVPP-2c, cc-pwCVTZ, dhf-QZVPP-2c, cc-pwCVQZ, cc-pwCV5Z. 对这些重元素体系, 要用dhf-QZVPP-2c基组才能得到高精度的键长和谐振频率, 但是对于解离能, 即使cc-pwCVQZ基组仍有一定误差.
易书禾 , 王繁 . 含旋轨耦合的耦合簇方法中的基组选择[J]. 化学学报, 2024 , 82(6) : 604 -612 . DOI: 10.6023/A24030081
Relativistic small-core energy-consistent pseudopotential is a commonly used method to deal with relativistic effects. Unfortunately, spin-orbit coupling effects (SOC) are generally not considered in developing basis sets for this pseudopotential except for the dhf-nZVPP-2c basis sets. Even the dhf-nZVPP-2c basis sets are validated mainly in density functional calculations. In this work, the SOC-CCSD(T) calculations with the scalar-relativistic Hartree-Fock determinant as reference using the small-core energy-consistent pseudopotential are carried out to investigate effects of 5s5p electrons and performance of various basis sets on properties and SOC effects of closed-shell diatomic molecules containing 6 row elements. Our results indicate that it is essential to include 5s5p electrons in SOC-CCSD(T) calculations to provide a reliable description on SOC effects. The cc-pVnZ-PP basis sets and the dhf-nZVPP basis set inadequately capture SOC effects, while the dhf-nZVPP-2c and cc-pwCVnZ-PP basis sets provide reasonable results. The error of these basis sets on properties of heavy-element systems aligns with the number of basis functions in these basis sets and the order is as follows: dhf-TZVPP-2c, cc-pwCVTZ, dhf-QZVPP-2c, cc-pwCVQZ, and cc-pwCV5Z. To obtain accurate bond lengths and harmonic vibrational frequencies of these heavy-element systems, at least the dhf-QZVPP-2c basis set should be employed. On the other hand, error of even the cc-pwCVQZ basis set is still sizeable for dissociation energies.

| [1] | Liu, W. J. J. Chem. Phys. 2024, 160, 084111. |
| [2] | Dyall, K. G.; F?gri, K. Introduction to Relativistic Quantum Chemistry, New York, 2007, Chapter III. |
| [3] | Douglas, M.; Kroll, N. M. Ann. Phys. 1974, 82, 89. |
| [4] | Liu, W. J.; Peng, D. J. Chem. Phys. 2006, 125, 044102. |
| [5] | Dolg, M.; Cao, X. Chem. Rev. 2012, 112, 403. |
| [6] | Bartlett, R. J.; Musia?, M. Rev. Mod. Phys. 2007, 79, 291. |
| [7] | Wang, F.; Gauss, J.; van Wüllen, C. J. Chem. Phys. 2008, 129, 064113. |
| [8] | Tu, Z.; Yang, D. D.; Wang, F.; Guo, J. J. Chem. Phys. 2011, 135, 034115. |
| [9] | Yang, D. D.; Wang, F. Phys. Chem. Chem. Phys. 2012, 14, 15816. |
| [10] | Guo, M. G.; Wang, Z. F.; Wang, F. Mol. Phys. 2020, 118, 19. |
| [11] | Cao, Z. L.; Wang, Z. F.; Yang, M. L.; Wang, F. Acta Phys.-Chim. Sin. 2014, 30, 431. (in Chinese) |
| [11] | (曹战利, 王治钒, 杨明理, 王繁, 物理化学学报, 2014, 30, 431.) |
| [12] | Cao, Z. L.; Wang, F.; Yang, M. L. J. Chem. Phys. 2016, 145, 154110. |
| [13] | Wang, Z. F.; Hu, S.; Wang, F.; Guo, J. W. J. Chem. Phys. 2015, 142, 144109. |
| [14] | Wang, Z. F.; He, B.; Lu, Y. Z.; Wang, F. Acta Chim. Sinica 2022, 80, 1401. (in Chinese) |
| [14] | (王治钒, 何冰, 路艳朝, 王繁, 化学学报, 2022, 80, 1401.) |
| [15] | Liang, Y. N.; Wang, F. Acta Phys.-Chim. Sin. 2014, 30, 1447. (in Chinese) |
| [15] | (梁艳妮, 王繁, 物理化学学报, 2014, 30, 1447.) |
| [16] | (a) Dolg, M. Chem. Phys. Lett. 1996, 250, 75. |
| [16] | (b) Dolg, M. J. Chem. Phys. 1996, 104, 4061. |
| [17] | Fantin, P. A.; Barbieri, P. L.; Canal Neto, A.; Jorge, F. E. Journal of Molecular Structure: THEOCHEM. 2007, 810, 103. |
| [18] | Lehtola, S.; Manninen, P.; Hakala, M.; H?m?l?inen, K. J. Chem. Phys. 2013, 138, 044109. |
| [19] | Jakobsen, P.; Jensen, F. J. Chem. Phys. 2019, 151, 174107. |
| [20] | Jensen, F. Theor. Chem. Acc. 2010, 126, 371. |
| [21] | Jensen, F. J. Chem. Theory Comput. 2008, 4, 719. |
| [22] | Ambroise, M. A.; Jensen, F. J. Chem. Theory Comput. 2019, 15, 325. |
| [23] | Bross, D. H.; Peterson, K. A. Theor. Chem. Acc. 2014, 133, 1434. |
| [24] | Peterson, K. A. J. Chem. Phys. 2015, 142, 074105. |
| [25] | Yannick, J. F.; Lucas, S.; Patrik, P.; Florian, W. J. Chem. Theory Comput. 2020, 16, 5658. |
| [26] | Cheng, L.; Gauss, J. J. Chem. Phys. 2011, 135, 084114. |
| [27] | Cao, Z. L.; Li, Z. D.; Wang, F.; Liu, W. J. Phys. Chem. Chem. Phys. 2017, 19, 3713. |
| [28] | Metz, B.; Stoll, H.; Dolg, M. J. Chem. Phys., 2000, 113, 2563. |
| [29] | Figgen, D.; Rauhut, G.; Dolg, M.; Stoll, H. Chem. Phys. 2005, 311, 227. |
| [30] | Lu, Y. Z.; Wang, Z. F.; Wang, F. J. Chem. Phys. 2023, 159, 244107. |
| [31] | Peterson, K. A.; Dunning, T. H. Jr. J. Chem. Phys. 2002, 117, 10548. |
| [32] | Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. |
| [33] | Armbruster, M. K.; Klopper, W.; Weigend, F. Phys. Chem. Chem. Phys. 2006, 8, 4862. |
| [34] | (a) Wang, F; Gauss, J. J. Chem. Phys. 2008, 129, 174110. |
| [34] | (b) Wang, F; Gauss, J. J. Chem. Phys. 2009, 131, 164113. |
| [35] | Metz, B.; Schweizer, M.; Stoll, H.; Dolg, M; Liu, W. J. Theor. Chem. Acc. 2000, 104, 22. |
| [36] | Peterson, K. A.; Figgen, D.; Goll, E.; Stoll, H.; Dolg, M. J. Chem. Phys. 2003, 119, 11113. |
| [37] | Peterson, K. A. J. Chem. Phys. 2003, 119, 11099. |
| [38] | Dunning, T. H. J. Chem. Phys. 1989, 90, 1007. |
| [39] | Weigend, F.; Filipp, F.; Reinhart, A. J. Chem. Phys. 2003, 119, 12753. |
| [40] | Peterson, K. A.; Yousaf, K. E. J. Chem. Phys. 2010, 133, 174116. |
| [41] | Liebman, J. F. J. Chem. Educ. 1973, 50, 831. |
| [42] | CFOUR, a quantum chemical program package written by Stanton, J. F.; Gauss, J.; Harding, M. E.; Szalay, P. G. with contributions from Auer, A. A.; Bartlett, R. J.; Benedikt, U.; Berger, C.; Bernholdt, D. E.; Bomble, Y. J.; Cheng, L.; Christiansen, O.; Heckert, M.; Heun, O.; Huber, C.; Jagau, T.-C.; Jonsson, D.; Juse′lius, J.; Klein, K.; Lauderdale, W. J.; Matthews, D. A.; Metzroth, T.; Mu¨ck, L. A.; O’Neill, D. P.; Price, D. R.; Prochnow, E.; Puzzarini, C.; Ruud, K.; Schiffmann, F.; Schwalbach, W.; Stopkowicz, S.; Tajti, A.; Va′zquez, J.; Wang, F.; Watts, J. D. and the integral packages MOLECULE (Almlo¨f, J. and Taylor, P. R.), PROPS (Taylor, P. R.), ABACUS (Helgaker, T.; Jensen, H. J. A.; J?rgensen, P. and Olsen, J.), and ECP routines by Mitin, A. V. and van Wu¨llen, C.. For the current version, see http://www.cfour.de. |
| [43] | Huber, K. P.; Herzberg, G. Molecular Spectra and Molecular Structure, Constants of Diatomic Molecules, Van Nostrand Rienhold, New York, 1979. |
| [44] | Sontag, H.; Weber, R. J. Mol. Spectrosc. 1982, 91, 72. |
| [45] | Effantin, C.; Topouzkhanian, A.; Figuet, J.; d’Incan, J.; Barrow, R. F.; Verges, J. J. Phys. B 1982, 15, 3829. |
/
| 〈 |
|
〉 |