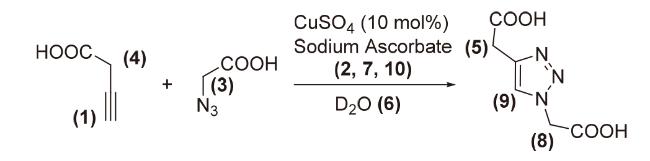
1 引言
在宏观尺度下, 定向运动是一种非常普遍的现象, 物体可以通过定向运动将某种形式的能量(如电能、化学能)转化为机械功, 我们可以利用这一点在宏观尺度上设计输入其他形式的能量、获得机械功的机器, 即马达. 然而当空间尺度缩小至纳米尺度时, 由于物体的尺寸已经接近所处区域的环境分子尺寸, 其处在粘度占主导地位的环境中, 在这种低雷诺数、过阻尼的条件下, 物体无法依靠惯性来维持运动; 同时向纳米尺度下的物体输入的能量会在短时间内耗散在布朗运动中, 难以像宏观物体那样转化为定向的机械功[1].
一个典型的例子是分子机器(Molecular Machine). 在过去的几十年里, 科学家们曾致力于研究一类天然的分子机器——马达蛋白(Motor Protein). 马达蛋白通过复杂的结构消耗能量, 执行多种多样的生物学功能, 典型的马达蛋白如肌球蛋白、微管蛋白、驱动蛋白、力感受器、三磷酸腺苷(Adenosine TriPhosphate, ATP)合酶等, 它们中的大部分都直接或间接地利用ATP水解的能量进行驱动, 少部分则依靠跨膜离子浓度梯度或者光照等方式提供能量[2]. 对马达蛋白的研究给了合成化学家启发, 他们设计并合成出了多样的人造分子马达, 如分子电梯(Elevators)、纳米汽车(Nanocars)、分子穿梭机(Shuttles)等[3]. 2016年, Jean-Pierre Sauvage、Sir J. Fraser Stoddart、Bernard L. Feringa三位科学家也因设计和合成分子机器荣获诺贝尔化学奖. 前面已经提到过在纳米尺度下, 分子热运动造成的能量损耗不可忽视, 以宏观视角为分子机器输入能量, 得到的结果与宏观世界也会截然不同. 因此了解这些高效的天然马达蛋白动力学原理是很有必要的. 研究人员相继提出了如动力冲程(Power Stroke)、布朗棘轮(Brownian Ratchet)等理论, 然而按照这些理论构建的人造分子机器的功效依然难以比肩天然马达蛋白[4].
2013年, Sen[5a]发现, 在烯烃闭环复分解反应中, 钌基Grubbs催化剂的扩散系数随着底物浓度的增加而增加; 因此, 他认为该Grubbs催化剂具有分子马达的性质, 将其称之为表现出催化驱动运动的最小单分子马达. Sen[5b-5c]为纳米尺度下的系统提出了一种理想方式的功能方式, 即化学催化反应, 而目前人造分子机器很少利用催化反应供能. 在此基础上越来越多的研究开始关注化学反应过程中相关分子的扩散性质, 希望能够研究这一过程的机制, 打破分子机器的功效限制. 在低雷诺数下, 对于溶液中自由扩散的粒子, 其扩散系数符合Stokes-Einstein关系, 即:
$D=\frac{k_{\mathrm{B}} T}{6 \pi \eta r}$
其中D为扩散系数, kB为玻尔兹曼常数, T为热力学温度, η为粘度系数, r为粒子的流体力学半径. 根据式(1), 可以算出粒子的扩散系数D; 当实测扩散系数Dexp与基于式(1)的计算结果不符, 即不满足Stokes-Einstein关系, 该扩散称为非Stokes-Einstein扩散或非经典扩散, 若实测扩散系数Dexp显著大于式(1)的计算结果, 这种扩散行为在研究中也常被称为“增强扩散”.
2020年, Granick课题组[6]使用核磁共振波谱的扩散序谱(Diffusion Ordered Spectroscopy, DOSY)研究了铜(I)催化环加成(Copper (I)-catalyzed Alkyne-Azide Cycloaddition, CuAAC)反应、Grubbs开环复分解聚合(Ring-Opening Metathesis Polymerization, ROMP)反应、Sonogashira偶联、Diels-Alder (D-A)反应、SN1反应与SN2反应中各物种的扩散系数, 结果表明在CuAAC反应中溶剂、底物、催化剂中均有非经典扩散的现象, 其中炔丙醇的扩散系数变化最大, 增加了60%以上, 其它物种如叠氮乙酸、溶剂重水、抗坏血酸也有不同程度的扩散系数增大. 作者还在不同反应物浓度下进行了相应的测试, 发现对于较高的反应物浓度时, 扩散系数变化的峰值对于催化剂而言没有变化但将持续更长时间, 对于溶剂而言有相应的增加. 催化剂表现出的非Stokes-Einstein扩散现象并不依赖于反应物浓度而与催化剂浓度成正相关, 表明该现象符合单粒子动力学的特征, 溶剂的扩散系数变化可能是由于反应中心与附近溶剂流体动力学相互作用的结果.
2023年, Wang课题组[7]使用单分子追踪(Single- Molecule Tracking, SMT)方法研究了CuAAC以及D-A反应过程中的扩散问题. 对于CuAAC反应, 作者使用了炔丙胺和叠氮乙酸作为反应物、碘化亚铜作为催化剂、2,6-二甲基吡啶作为配体进行反应, 研究人员将炔基封端的ATTO 647N荧光探针(以下简称为荧光炔)掺杂入反应物中进行荧光示踪, 结果表明, CuAAC反应过程中, 炔以及产物分子的扩散系数增加了约20%; D-A反应过程中受方法测量检测限所限制则没有观察到明显的非Stokes-Einstein扩散现象. 研究人员还发现, 当反应物浓度低于0.03 mol•L－1或催化剂浓度低于0.2 mmol•L－1后, 无法检测到显著的非Stokes-Einstein扩散. 作者讨论了各种可能的扩散增强机制, 如自电泳、热效应、对流等等, 然而这些机制在具体细节上无法与实验结果完全匹配, 说明非Stokes-Einstein扩散并非由于非反应因素引起的, 是与化学反应耦合的, 研究人员进行了密度泛函理论计算和分子动力学模拟, 结果表明该现象与溶剂的氢键反应网络的动态变化相关.
非经典扩散现象的研究此前也受到了一些质疑, 一般认为化学键的形成/断裂(即化学反应)的时间尺度在fs~ps量级, 而分子扩散行为的时间尺度在μs~ms量级, 非经典扩散现象违背了长期以来认为化学反应与扩散相互正交的认识. Günther等[8a]认为化学反应导致的1H信号强度变化造成了DOSY测定过程中的伪影, 从而出现了伪扩散增强现象; Fillbrook等[8b]指出CuAAC反应中Cu(I)作为顺磁性物种会导致时间依赖的弛豫速率, 造成DOSY测定过程中的伪影; Rezaei-Ghaleh等[8c]开发了新的扩散核磁共振方法, 发现当叠氮化物不存在时, 作为CuAAC反应的两种反应物之一的炔的扩散系数并没有下降, 故此他们认为结果并不支持催化诱导的增强扩散现象; Beves等[8d]则提出该现象是由于反应过程中的热量释放导致的局部热对流的简单结果. 对上述疑问, Wang等[9]进行了随机梯度场强度序列DOSY实验和加入顺磁弛豫剂Gd-EDTA的DOSY实验, 结果表明非经典扩散现象仍然存在, 同时不存在顺磁物种的D-A反应也能观察到非经典扩散, 说明该现象是真实存在的, 并不是分析方法导致的伪影. 根据能均分定理, 当一个系统处于热平衡状态时, 其动能被等量分配到每个符合麦克斯韦-玻尔兹曼分布的自由度上, 即对于一个具有f个转动自由度的分子来说, 其3个自由度上的平动能与f个自由度上的转动能相等. 分子的实际运动是平动与转动的耦合, 尽管化学反应过程是典型的非平衡态, 但平动与转动的联系依旧存在, 如果认为该现象是由简单热对流导致的, 那么在分子的转动自由度上应当能够观察到扩散系数增大, 因此我们认为有必要对化学反应中分子的转动扩散性质进行研究, 尝试阐明非经典扩散现象的机制并回应此前的一些质疑.
用于检测分子转动扩散的常规方法包括核磁共振波谱(Nuclear Magnetic Resonance spectroscopy, NMR)、荧光各向异性/偏振(Fluorescence Anisotropy/Polari- zation, FA/FP)以及介电光谱(Dielectric Spectroscopy, DS)等方法[10]. NMR是研究分子转动扩散性质中最常用的方法, 主要利用转动相关时间与弛豫速率之间的关系, 通过T1反转恢复实验(T1 inversion recovery, T1IR)对分子的转动扩散进行研究[11]. FA与FP则是依赖于荧光团对线偏振光激发下, 发光偏振方向的退偏程度不同, 求得转动扩散系数[12]. 分子转动会影响极化矢量与弛豫时间, 进而影响介电性质, 因此也可以用某些情况下DS来研究分子的转动扩散系数[13].
基于此, 本组采用核磁共振氢谱弛豫检测作为研究手段, 对如下图1所示的CuAAC反应进行了时间分辨的转动扩散研究, 并结合荧光各向异性作为独立的检测方法, 对核磁共振的结果进行了校验.
2 结果与讨论
2.1 CuAAC反应过程中转动扩散系数减小
为了确认该反应存在平动维度的非经典扩散现象, 我们在底物浓度为230 mmol/L的条件下进行了DOSY实验. 为了表征扩散系数变化幅度, 以分子在自由状态下的扩散系数D0为基准, 计算扩散系数变化相对值.
$\frac{\Delta D}{D_{0}}=\frac{D_{\exp }-D_{0}}{D_{0}}$
结果如图2所示, 可以看到在反应初期底物3-丁炔酸和叠氮乙酸的平动扩散系数明显增大并随反应进行逐渐衰减, 产物2,2'-(1H-1,2,3-三唑-1,4-二基)二乙酸(以下简称三氮唑)反应初期没有平动扩散系数的明显增大.
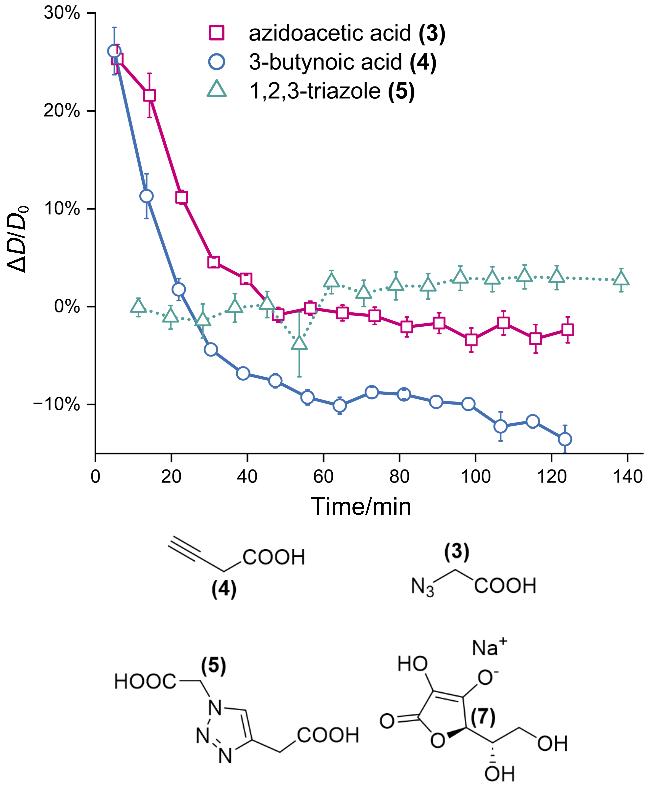
图2 CuAAC反应过程中平动扩散系数随时间的变化. 数字对应于拟合扩散系数所用的核磁1H信号, 3-丁炔酸与叠氮乙酸的起始浓度为230 mmol/L, CuSO4浓度为10 mol%, 抗坏血酸钠浓度为40 mol%Figure 2 Translational diffusion coefficients plotted as a function of time during the CuAAC reaction. Numbers correspond to the 1H signal used to fit the translational diffusion coefficient, the starting concentration of 3-butynoic acid and azidoacetic acid were both 230 mmol/L, the concentration of CuSO4 was 10 mol% of the reactant, and the concentration of sodium ascorbate was 40 mol% of the reactant |
当自旋量子数I为1/2的核置于外部磁场B0中时, 存在两个塞曼能级, 布居数符合玻尔兹曼分布. 布居数的差异会产生净的宏观磁化矢量MI, 并与B0平行. 当施加射频脉冲时, 有效磁场变为B, 塞曼能级会重建平衡, 宏观磁化矢量的演化符合单指数形式, 遵循下式:
$M_{z}(t)=M_{z}(0) \exp \left(-\frac{t}{T_{1}}\right)$
其中Mz(0)是在磁场B0下的初始磁化, T1即自旋-晶格弛豫时间; 其倒数R1为自旋-晶格弛豫速率[14].
在理想情况下, 可以近似认为R1只与转动相关时间τrot有关, 则
$R_{1}(\omega)=\frac{3}{10}\left(\frac{\mu_{0}}{4 \pi} \frac{\gamma^{2} \hbar}{r^{3}}\right)^{2}\left(\frac{\tau_{\mathrm{rot}}}{1+\left(\omega \tau_{\mathrm{rot}}\right)^{2}}+\frac{4 \tau_{\mathrm{rot}}}{1+\left(2 \omega \tau_{\mathrm{rot}}\right)^{2}}\right)$
其中μ0和ℏ分别为磁导率和约化普朗克常数, r为自旋间距, ω为拉莫尔频率, γ为旋磁比[15]. 典型的小分子的τrot在ps量级, ω则对应于所用NMR谱仪的磁场强度, 一般在几百MHz, 则小分子的ωτrot<<1, 此时可以认为R1与τrot成正比.
根据Einstein关系, 分子的转动扩散系数Dr可以描述为[16]
$D_{\mathrm{r}}=\frac{\mathrm{k}_{\mathrm{B}} T}{8 \pi \eta r^{3}}=\tau_{\mathrm{rot}}^{-1}$
由此, T1与Dr近似成正比, 根据T1IR实验测定反应过程中分子的T1即可得知反应过程中Dr的变化, 则(ΔD/D0)r为
$\left(\frac{\Delta D}{D_{0}}\right)_{\mathrm{r}}=\frac{T_{1, \exp }-T_{1,0}}{T_{1,0}}$
为了获得更好的时间依赖动力学信息, 需要在保证NMR谱图质量的情况下, 尽可能缩短采集周期, 为此我们对脉冲序列进行了优化, 可以将单组实验时间压缩至8 min左右(见支持信息, 图S3). 在不同的反应物浓度下进行了T1IR实验, 结果如图3所示.
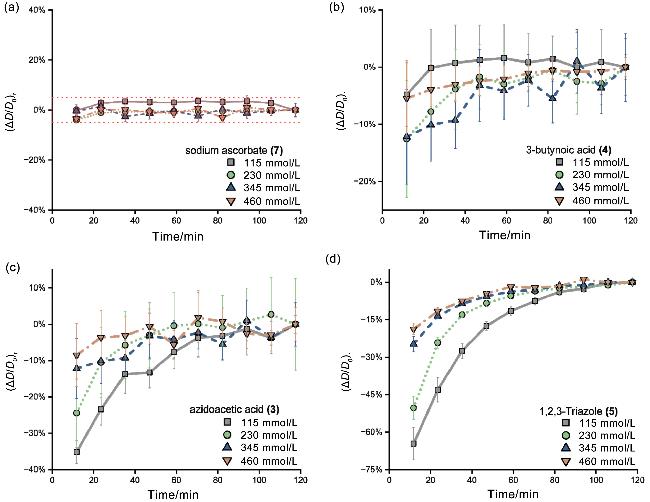
图3 不同浓度下CuAAC反应过程中转动扩散系数随时间的变化. 图中浓度为反应物起始浓度. (a)基于抗坏血酸钠的(7)信号拟合的转动扩散系数随时间的变化; (b)基于3-丁炔酸的(4)信号拟合的转动扩散系数随时间的变化; (c)基于叠氮乙酸的(3)信号拟合的转动扩散系数随时间的变化; (d)基于三氮唑的(5)信号拟合的转动扩散系数随时间的变化.Figure 3 Rotational diffusion coefficient over time during CuAAC reaction at different concentrations. The concentrations in the figure are the starting concentrations of the reactants. (a) Rotational diffusion coefficients of sodium ascorbate over time, fitted with the NMR signals of (7); (b) rotational diffusion coefficients of 3-butynoic acid over time, fitted with the NMR signals of (4); (c) rotational diffusion coefficients of azidoacetic acid plotted as a function of time, fitted with the NMR signals of (3); (d) rotational diffusion coefficients plotted as a function of time of 1,2,3-triazole, fitted with the NMR signals of (5) |
由于分子的扩散系数受温度、粘度等环境因素影响, 了解在整个反应过程中的环境因素变化非常重要. 根据CuAAC反应机理[17], 反应起始Cu(II)被还原为Cu(I), 之后由抗坏血酸钠维持还原性氛围, 可以认为在反应过程中抗坏血酸钠是惰性物种, 其Dr的变化可以反映环境因素的变化. 测定抗坏血酸钠的Dr随时间变化如图3a所示, 变化不显著, 所以测定过程中环境因素对扩散系数的影响可以忽略. 可以看到在反应初期, 底物3-丁炔酸、叠氮乙酸和产物三氮唑出现了Dr的明显减小(图3b~3d). 不同浓度的实验结果表明3-丁炔酸和叠氮乙酸Dr变化与初始投料浓度相关性不显著, 而三氮唑在反应初期Dr与初始投料浓度正相关. 这一结果说明Dr的变化很可能与局部的反应中心有关, 因为在Dr变化最显著的反应初期产物的生成发生在反应活性中心的区域.
我们对CuAAC反应进行了FA实验以进一步确认分子在反应中的转动扩散情况, 以偏振光激发荧光偶极子, 测量其在水平和垂直偏振平面上的荧光发射, 并基于垂直激发偏振平面的荧光强度I⊥和平行激发偏振平面的荧光强度I∥可以计算荧光各向异性r:
$r=\frac{I_{\|}-I_{\perp}}{I_{\|}+2 I_{\perp}}$
荧光团在激发和发射时间间隔内的旋转会导致发射的去偏振. 根据Perrin方程, 这个过程中荧光各向异性r满足如下关系:
$\frac{1}{r}=\frac{1}{r_{0}}\left(1+\frac{\tau_{\mathrm{F}}}{\tau_{\mathrm{rot}}}\right)$
其中, r0为荧光基团不旋转时的各向异性, τF为荧光寿命, τrot为转动相关时间[18], 由此可知分子转动越快, τrot越小, r越接近0.
反应结束后r并没有回到无反应状态的基准值, 这是由于FA实验只能给出反应过程中荧光团的r变化, CuAAC反应并不改变荧光团的结构, 因此FA实验无法区分r来自反应物炔烃还是产物三氮唑, 但可以观察到在40 min之后r已经进入稳定的平台期, 且反应初期的r远高于基准值. 由于NMR的实验结果已经指出, 反应物和产物的变化趋势是一致的, 因此在该实验中, FA的结果可以用于独立校验NMR的结果.
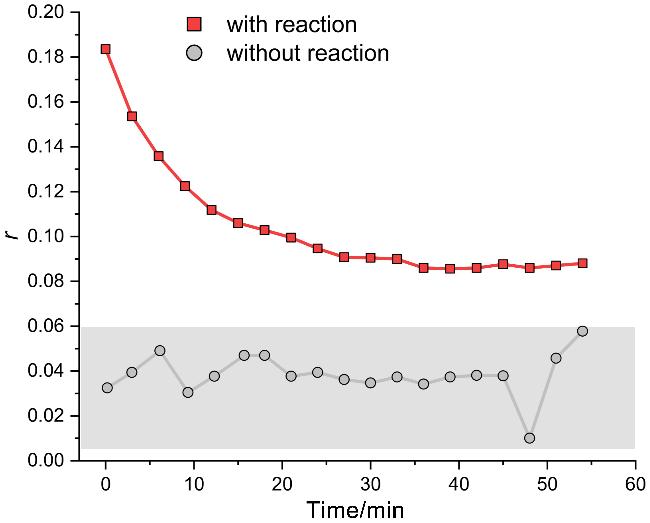
2.2 反应过程中非经典转动扩散现象原因的讨论
化学反应中的能量释放速率通常被认为是一个引起平动扩散增强可能的因素, 根据DOSY实验结果可以看到, T1与反应速率之间存在一定的正相关性, 但没有明确的函数关系. 如果认为能量释放导致的热对流引起了平动扩散系数的变化, 无法解释为何反应过程中会出现转动扩散系数减小的现象, 没有理由认为化学反应释放出的能量可以定向的转变为平动能, 所以反应过程中非布朗扩散现象不是或不完全是能量释放导致的.
T1IR实验结果已经证明反应过程中环境粘度和温度没有显著改变, 假定在反应过程中分子的流体力学半径没有显著变化, 那么根据Stokes-Einstein关系, 扩散系数变化相对值实际上反映了在平动维度和转动维度上的能量变化, 即ΔD/D0实际上代表了平动和转动维度上的Δ(kBT)/(kBT)0, 其随反应进程的变化如图5a. 可以看到反应物分子的平动和转动扩散系数变化在反应进程的时间尺度上具有强相关性, 说明非经典扩散现象是与反应进程耦合的. 现有研究一般认为CuAAC的催化循环中, 反应中底物炔会先与Cu(I)形成单核和双核炔- [Cu]络合物(图5b), 随后底物叠氮与炔-[Cu]络合物配位形成炔-[Cu]-叠氮活性络合物, 之后该活性络合物经由环状过渡态发生环加成反应并发生解离生成产物三氮唑和Cu(I)催化剂(图5b)[17]. 在这个过程中需要叠氮乙酸与3-丁炔酸在同一平面附近以特定的取向形成五元环以进入环加成过渡态, 这种定向性会导致分子的转动受限, 表现为分子转动变慢, 这与我们观察到的结果是相符的.
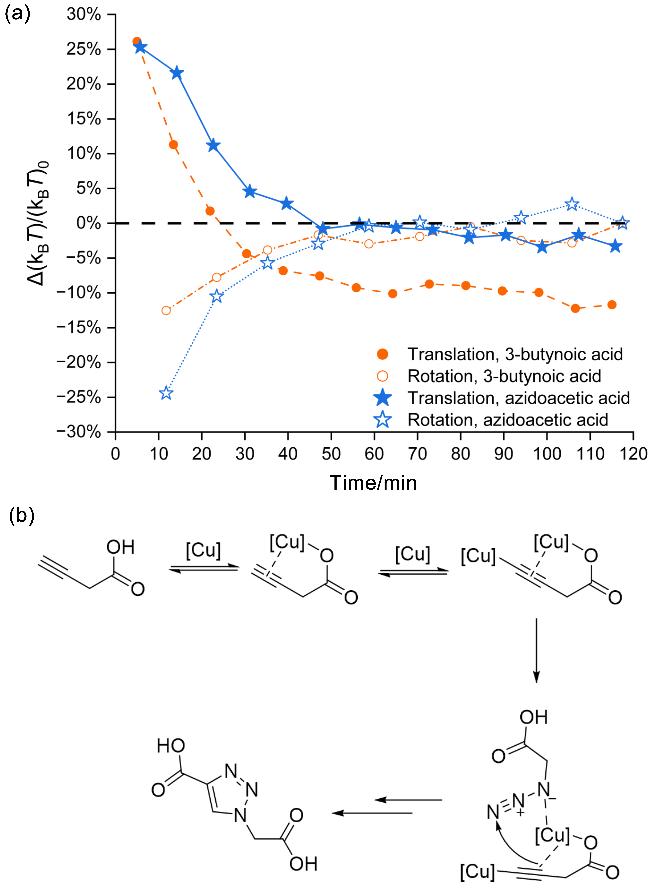
图5 平动能量和转动能量变化的可能机制. (a)反应过程中3-丁炔酸和叠氮乙酸平动和转动能量改变幅度随时间的变化; (b)可能的反应机理和中间体[17b]Figure 5 Possible mechanisms for the translational and rotational energy interconversion. (a) Change of translational and rotational energy ploted as a function of time during the reaction for 3-butynoic acid and azidoacetic acid; (b) proposed reaction mechanisms and reaction intermediates.[17b] |
前面已经提到, Granick课题组[6]的研究表明扩散系数变化的峰值与催化剂浓度相关而与反应物浓度无 关, 这说明CuAAC反应是扩散控制的. 根据经典的理论, 化学反应的时间尺度通常在ns量级, 而NMR采集的原始时域信号时间分辨率则在ms量级, 与反应时间尺度不匹配, 但我们已经明确该过程与化学反应的发生有关, 且这种现象同时出现于反应物和产物, 因此我们推测, 在过渡态前后, 由于某种机制使得分子在进入过渡态前的至少ms量级的时间, 即进行了一定程度上的对齐, 且过渡态中的定向性在形成产物后维持了至少ms量级的时间.
由图5a可以看出, 对于叠氮乙酸, 其转动能的减小幅度与平动能的增加幅度在检测的各个时间点基本一致, 由此我们推测在形成过渡态的过程中, 如果排除该反应释放的能量, 分子的总动能是守恒的, 分子减少的转动能转变为了其平动能. 对于3-丁炔酸, 其转动能变化与平动能变化在时间上高度吻合, 但在幅度上不是非常匹配, 从机理上看, 叠氮乙酸在与Cu配位后随即发生反应进入环状过渡态, 3-丁炔酸则相对更“早”与Cu配位, 在溶液中反应物-Cu络合物不是孤立分子, 而是与周围的水分子形成的反应物-溶剂复合物整体, 这使得3-丁炔酸的能量转换相对较复杂, 所以转动能与平动能变化在幅度上存在差异, 这与Granick课题组[6]的研究中发现不参与反应的溶剂分子也存在非经典扩散现象以及Wang课题组[7]提出的非经典扩散现象与反应 物-溶剂氢键网络相关是相符的.
3 结论
综上, 在此前对化学催化反应中各物种的非Stokes-Einstein扩散现象研究的基础上, 我们研究了CuAAC反应的转动扩散系数在反应过程中的变化. 通过T1IR实验和FA/FP实验, 我们发现3-丁炔酸和叠氮乙酸在Cu(I)的催化下发生Click反应生成1,2,3-三氮唑类化合物的过程中, 底物和产物的转动扩散系数均有不同程度的减弱, 即分子的旋转速度减慢, 转动能减小, 存在非经典的转动扩散动力学. 基于此, 我们认为在反应过渡态形成之前的一段时间内, 反应物分子和催化剂分子发生了空间程度上的定向对齐, 导致了其转动速率的减慢. 结合此前研究表明CuAAC反应中各物种平动扩散系数有一定程度的增大, 我们认为在这个过程中分子失去的转动能转变为了分子的平动能.
本工作通过研究CuAAC反应过程中的转动扩散行为为研究化学催化反应中的非经典扩散现象提供了新的视角. 但需要指出在反应过程中, 不仅有分子本身的动能改变, 还伴随有反应吸收或释放能量, 同时还要考虑到反应中心复杂的溶剂复合物结构, 这几者是相互耦合的, 鉴于CuAAC反应较复杂的反应机理, 在现有结果下我们难以完整地描述CuAAC反应中的能量转化图景, 但我们希望后续通过改进现有分析方法或引入其他分析手段, 比如原位时空分辨的直接成像、分子动力学模拟与DFT计算等, 阐明催化反应非经典扩散现象的机制.
(Cheng, F.)