

基于图形处理单元与密度拟合近似的单精度耦合簇CCSD和CCSD(T)程序
收稿日期: 2022-07-17
网络出版日期: 2022-08-18
基金资助
四川省自然科学基金(2022NSFSC1262); 国家自然科学基金(21973063); 国家自然科学基金(21703020); 成都师范学院人才引进项目(2021YJRC202020)
Single-precision CCSD and CCSD(T) Calculations with Density Fitting Approximations on Graphics Processing Units
Received date: 2022-07-17
Online published: 2022-08-18
Supported by
Natrual Science Foundation of Sichuan Province(2022NSFSC1262); National Natural Science Foundation of China(21973063); National Natural Science Foundation of China(21703020); Foundation of Chengdu Normal University Talent Introduction Research Funding(2021YJRC202020)
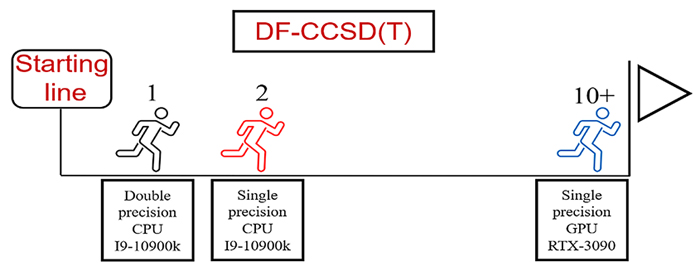
作者此前工作表明, 在耦合簇CCSD (Coupled-Cluster approaches within the singles and doubles approximation)与CCSD(T) (CCSD approaches augmented by a perturbative treatment of triple excitations)计算中结合单精度数与消费型图形处理单元(GPU), 可以显著提高计算速度. 然而由于CCSD(T)计算对内存的巨大需求以及消费型GPU的内存限制, 在利用消费型GPU进行加速时, 不考虑利用空间对称性的情况下, 此前开发的CCSD(T)程序仅能用于计算300~400个基函数的体系. 利用密度拟合(Density-Fitting, DF)处理双电子积分可以显著降低CCSD(T)计算过程中的内存需求, 本工作发展了基于密度拟合近似并结合单精度数进行运算的DF-CCSD(T)程序, 该程序可用于包含700个基函数的无对称性体系的单点能计算, 以及包含1700个基函数的有对称性体系. 本工作所使用的计算节点配置了型号为Intel I9-10900k的CPU和型号为RTX3090的GPU, 与用双精度数在CPU上的计算相比, 利用单精度数结合GPU进行运算可以将CCSD的计算速度提升16倍, (T)部分可提升40倍左右, 而使用单精度数引入的误差可忽略不计. 在程序开发过程中, 作者发展了一套可利用GPU或CPU结合单精度数或双精度数进行含空间对称性的矩阵操作代码库. 基于该套代码库, 可以显著降低开发含空间对称性的耦合簇代码的难度.
关键词: 耦合簇; 密度拟合; 图形处理单元(GPU); 单精度
王治钒 , 何冰 , 路艳朝 , 王繁 . 基于图形处理单元与密度拟合近似的单精度耦合簇CCSD和CCSD(T)程序[J]. 化学学报, 2022 , 80(10) : 1401 -1409 . DOI: 10.6023/A22070313
It has been reported by our group that using single-precision data and consumer graphics processing units (GPUs) can significantly improve computation speed of CCSD (Coupled-Cluster approaches within the singles and doubles approximation) and CCSD(T) (CCSD approaches augmented by a perturbative treatment of triple excitations). However, CCSD(T) can only be employed for small molecules with about 300~400 basis functions when using consumer GPUs for acceleration without spatial symmetry due to the memory limitation of GPU. Using density-fitting approximation can significantly reduce the memory requirements in CCSD(T) calculations. In this paper, DF-CCSD(T) codes based on the density fitting approximation together with single precision data was developed. All the matrix contractions were performed employing GEMM in CUBLAS on GPU or in Intel MKL on CPU. The other operations such as matrix expansion and transpose were performed using OpenACC on GPU or OpenMP on CPU. Those codes can be applied to single point energies for systems with around 700 basis functions without spatial symmetry and to molecules with about 1700 basis functions with symmetry on a GPU with 24 Gb memory. The server employed in this work has an Intel I9-10900k CPU and a RTX3090 GPU. CCSD calculations with single-precision data on GPU are about 16 times faster and it is about 40 times faster for the (T) part compared with the calculations on CPU using double precision data on this server. Error introduced by single precision data is negligible. A code library that can employ GPU or CPU using either single precision or double precision data to perform matrix operations with spatial symmetry was also reported in this work. Direct product decomposition (DPD) method was employed to deal with spatial symmetry. Complexity of developing coupled cluster codes with spatial symmetry can be significantly reduced with this library. The computational accuracy of single precision DF-CCSD(T) was compared with CCSD(T)-F12a and DLPNO-CCSD(T). The results shown that DF-CCSD(T) would be more stable than the other two approaches in describing chemical properties.

| [1] | Bartlett, R. J.; Musiał, M. Rev. Mod. Phys. 2007, 79, 291. |
| [2] | Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. Chem. Phys. Lett. 1989, 157, 479. |
| [3] | Řezáč, J.; Hobza, P. J. Chem. Theor. Comput. 2013, 9, 2151. |
| [4] | (a) Vahtras, O.; Almlöf, J.; Feyereisen, M. W. Chem. Phys. Lett. 1993, 213, 514. |
| [4] | (b) Van Alsenoy, C. J. Comput. Chem. 1988, 9, 620. |
| [5] | (a) Kats, D.; Korona, T.; Schütz, M. J. Chem. Phys. 2007, 127, 064107. |
| [5] | (b) Korona, T.; Jeziorski, B. J. Chem. Phys. 2008, 128, 144107. |
| [5] | (c) Boström, J.; Pitoňák, M.; Aquilante, F.; Neogrády, P.; Pedersen, T. B.; Lindh, R. J. Chem. Theor. Comput. 2012, 8, 1921. |
| [5] | (d) DePrince, A. E.; Sherrill, C. D. J. Chem. Theor. Comput. 2013, 9, 2687. |
| [5] | (e) Epifanovsky, E.; Zuev, D.; Feng, X.; Khistyaev, K.; Shao, Y.; Krylov, A. I. J. Chem. Phys. 2013, 139, 134105. |
| [5] | (f) DePrince, A. E.; Kennedy, M. R.; Sumpter, B. G.; Sherrill, C. D. Mol. Phys. 2014, 112, 844. |
| [5] | (g) Lesiuk, M. J. Chem. Phys. 2020, 152, 044104. |
| [5] | (h) Bozkaya, U.; Sherrill, C. D. J. Chem. Phys. 2017, 147, 044104. |
| [5] | (i) Shen, T.; Zhu, Z.; Zhang, I. Y.; Scheffler, M. J. Chem. Theor. Comput. 2019, 15, 4721. |
| [6] | (a) Harvey, M. J.; De Fabritiis, G. WIREs: Comput. Mol. Sci. 2012, 2, 734. |
| [6] | (b) Walker, R. C.; Götz, A. W. Electronic Structure Calculations on Graphics Processing Units. (Wiley Online Library, 2016). |
| [6] | (c) Bao, J. Z.; Feng, X. T.; Yu, J. G. Acta Phys. Chim. Sin. 2011, 27, 2019. (in Chinese) |
| [6] | (鲍建樟, 丰鑫田, 于建国, 物理化学学报, 2011, 27, 2019.) |
| [7] | (a) Stopper, D.; Roth, R. J. Chem. Phys. 2017, 147, 064508. |
| [7] | (b) Nitsche, M. A.; Ferreria, M.; Mocskos, E. E.; Gonzalez Lebrero, M. C. J. Chem. Theor. Comput. 2014, 10, 959. |
| [7] | (c) Jia, W.; Fu, J.; Cao, Z.; Wang, L.; Chi, X.; Gao, W.; Wange, L. W. J. Comput. Phys. 2013, 251, 102. |
| [7] | (d) Genovese, L.; Ospici, M.; Deutsch, T.; Mehaut, J. F.; Neelov, A.; Goedecker, S. J. Chem. Phys. 2009, 131, 034103. |
| [8] | (a) Tornai, G. J.; Ladjanszki, I.; Rak, A.; Kis, G.; Cserey, G. J. Chem. Theor. Comput. 2019, 15, 5319. |
| [8] | (b) Rak, A.; Cserey, G. Chem. Phys. Lett. 2015, 622, 92. |
| [8] | (c) Asadchev, A.; Gordon, M. S. J. Chem. Theor. Comput. 2012, 8, 4166. |
| [8] | (d) Wang, Y.; Tian, Y. Q.; Jin, Z.; Suo, B. B. Acta Chim. Sinica 2021, 79, 653. (in Chinese) |
| [8] | (王岩, 田英齐, 金钟, 索兵兵, 化学学报, 2021, 79, 653.) |
| [9] | (a) Bykov, D.; Kjaergaard, T. J. Comput. Chem. 2017, 38, 228. |
| [9] | (b) Angel Martinez-Martinez, L.; Amador-Bedolla, C. J. Mex. Chem. Soc. 2017, 61, 60. |
| [9] | (c) Song, C.; Martinez, T. J. J. Chem. Phys. 2016, 144, 174111. |
| [9] | (d) Maurer, S. A.; Kussmann, J.; Ochsenfeld, C. J. Chem. Phys. 2014, 141, 051106. |
| [10] | Fales, B. S.; Levine, B. G. J. Chem. Theor. Comput. 2015, 11, 4708. |
| [11] | Fales, B. S.; Curtis, E. R.; Johnson, K. G.; Lahana, D.; Seritan, S.; Wang, Y.; Weir, H.; Martínez, T. J.; Hohenstein, E. G. J. Chem. Theor. Comput. 2020, 16, 2021. |
| [12] | Knizia, G.; Li, W.; Simon, S.; Werner, H. J. J. Chem. Theor. Comput. 2011, 7, 2387. |
| [13] | Pokhilko, P.; Epifanovsky, E.; Krylov, A. I. J. Chem. Theor. Comput. 2018, 14, 4088. |
| [14] | Wang, Z.; Guo, M.; Wang, F. Phys. Chem. Chem. Phys. 2020, 22, 25103. |
| [15] | Knizia, G.; Adler, T. B.; Werner, H.-J. J. Chem. Phys. 2009, 130, 054104. |
| [16] | (a) Guo, Y.; Riplinger, C.; Becker, U.; Liakos, D. G.; Minenkov, Y.; Cavallo, L.; Neese, F. J. Chem. Phys. 2018, 148, 011101. |
| [16] | (b) Liakos, D. G.; Guo, Y.; Neese, F. J. Phys. Chem. A 2020, 124, 90. |
| [17] | Gauss, J.; Stanton, J. F.; Bartlett, R. J. J. Chem. Phys. 1991, 95, 2623. |
| [18] | (a) Sun, Q.; Berkelbach, T. C.; Blunt, N. S.; Booth, G. H.; Guo, S.; Li, Z.; Liu, J.; McClain, J. D.; Sayfutyarova, E. R.; Sharma, S.; Wouters, S.; Chan, G. K.-L. WIREs Comput. Mol. Sci. 2018, 8, 1340. |
| [18] | (b) Sun, Q.; Zhang, X.; Banerjee, S.; Bao, P.; Barbry, M.; Blunt, N. S.; Bogdanov, N. A.; Booth, G. H.; Chen, J.; Cui, Z.-H.; Eriksen, J. J.; Gao, Y.; Guo, S.; Hermann, J.; Hermes, M. R.; Koh, K.; Koval, P.; Lehtola, S.; Li, Z.; Liu, J.; Mardirossian, N.; McClain, J. D.; Motta, M.; Mussard, B.; Pham, H. Q.; Pulkin, A.; Purwanto, W.; Robinson, P. J.; Ronca, E.; Sayfutyarova, E. R.; Scheurer, M.; Schurkus, H. F.; Smith, J. E. T.; Sun, C.; Sun, S.-N.; Upadhyay, S.; Wagner, L. K.; Wang, X.; White, A.; Whitfield, J. D.; Williamson, M. J.; Wouters, S.; Yang, J.; Yu, J. M.; Zhu, T.; Berkelbach, T. C.; Sharma, S.; Sokolov, A. Y.; Chan, G. K.-L. J. Chem. Phys. 2020, 153, 024109. |
| [19] | Dunning, T. H. J. Chem. Phys. 1989, 90, 1007. |
| [20] | Weigend, F. Phys. Chem. Chem. Phys. 2002, 4, 4285. |
| [21] | (a) Peterson, K. A.; Figgen, D.; Goll, E.; Stoll, H.; Dolg, M. J. Chem. Phys. 2003, 119, 11113. |
| [21] | (b) Peterson, K. A.; Shepler, B. C.; Figgen, D.; Stoll, H. J. Phys. Chem. A 2006, 110, 13877. |
| [22] | Figgen, D.; Rauhut, G.; Dolg, M.; Stoll, H. Chem. Phys. 2005, 311, 227. |
| [23] | Stoychev, G. L.; Auer, A. A.; Neese, F. J. Chem. Theor. Comput. 2017, 13, 554. |
| [24] | Peverati, R.; Truhlar, D. G. Philos. T. R. Soc. A 2014, 372, 20120476. |
| [25] | Werner, H.-J.; Knowles, P. J.; Manby, F. R.; Black, J. A.; Doll, K.; Heßelmann, A.; Kats, D.; Köhn, A.; Korona, T.; Kreplin, D. A.; Ma, Q.; Miller, T. F.; Mitrushchenkov, A.; Peterson, K. A.; Polyak, I.; Rauhut, G.; Sibaev, M. J. Chem. Phys. 2020, 152, 144107. |
| [26] | Neese, F. WIREs Comput. Mol. Sci. 2012, 2, 73. |
/
| 〈 |
|
〉 |